
【题目】己知如图,等腰![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .点
.点![]() 是延长线上一点,点
是延长线上一点,点![]() 是线段上一点,
是线段上一点,![]() 下面的结论: ①
下面的结论: ①![]() ;②
;②![]() ;③
;③![]() 是等边三角形④.
是等边三角形④.![]() 其中正确的是( )
其中正确的是( )
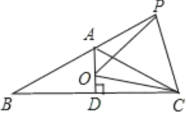
A. ①③④B. ①②③C. ①③D. ①②③④
【答案】A
【解析】
①利用等边对等角,即可证得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;
②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;
③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;
④首先证明△OPA≌△CPE,则AO=CE,AB=AC=AE+CE=AO+AP.
解:①如图,连接OB,
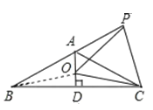
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°∠BAD=30°
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;故①正确;
②由①知:∠APO=∠ABO,∠DCO=∠DBO,
∵点O是线段AD上一点,
∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;
③∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;故③正确;
④如图,在AC上截取AE=PA,连接PB,
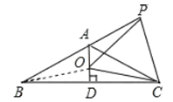
∵∠PAE=180°∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
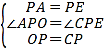 ,
,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AB=AC=AE+CE=AO+AP;故④正确;
本题正确的结论有:①③④,
故选:A.


科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮参加中华诗词大赛,还剩最后两题,如果都答对,就可顺利通关.其中第一道单选题有4个选项,第二道单选题有3个选项.小亮这两道题都不会,不过还有一个“求助”没有使用(使用求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小亮第一题使用“求助”,那么他答对第一道题的概率是__;
(2)他的亲友团建议:最后一题使用“求助”,从提高通关的可能性的角度看,你同意亲友团的观点吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一口袋中装有四根长度分别为1 cm,3 cm,4 cm,5 cm的细木棒,小明手中有一根长度为3 cm的细木棒,现随机从口袋中取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:
(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修站,甲小组乘坐一辆汽车,沿东西方向的公路进行检修线路,约定向东为正,从![]() 地出发到收工时,行走记录为(单位:
地出发到收工时,行走记录为(单位:![]() ): +8,- 2, -13, -1, +10.同时,乙小组也从
): +8,- 2, -13, -1, +10.同时,乙小组也从![]() 地出发, 沿南北方向的公路检修线路,约定向北为正,行走记录为: -7, +9,- 2, +8,- 6.
地出发, 沿南北方向的公路检修线路,约定向北为正,行走记录为: -7, +9,- 2, +8,- 6.
(1)分别计算收工时,甲,乙两组各在![]() 地的哪一边,分别距离
地的哪一边,分别距离![]() 地多远?
地多远?
(2)若每千米汽车汽油消耗为0.3![]() ,求出发到收工时两组各耗油多少升?
,求出发到收工时两组各耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
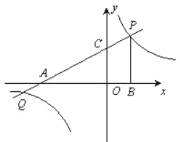
【题目】如图,直线y=0.5x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=kx-1在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
(1)求反比例函数的解析式;
(2)求△APB的面积;
(3)求在第一象限内,当x取何值时一次函数的值小于反比例函数的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com