
【题目】如图,在平面直角坐标系中,O为坐标原点,点A在反比例函数y=![]() (x > 0)的图象上,作AB⊥y轴于B点.
(x > 0)的图象上,作AB⊥y轴于B点.
(1) △ABO的面积为 .
(2) 若点A的横坐标为4,点P在x轴的正半轴.且△OAP是等腰三角形,求点P的坐标: .
(3)动点M从原点出发,沿x轴的正方向运动,以MA为直角边,在MA的右侧作等腰Rt△MAN=90°,若在点M运动过程中,斜边MN始终在x轴上,求ON-OM的值
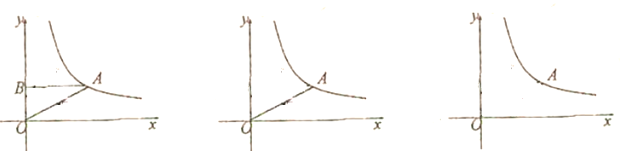
【答案】(1)6;(2)(5,0)或(8,0)或(![]() ,0);(3)48.
,0);(3)48.
【解析】
(1)根据反比例函数系数k的几何意义,即可求出△ABO的面积;
(2)先求出点A的坐标,设点P的坐标为(a,0)由题意可知:a>0,根据平面直角坐标系中任意两点之间的距离公式,即可求出OA=![]() ,OP=a,AP=
,OP=a,AP=![]() ,然后根据等腰三角形的腰的情况分类讨论即可;
,然后根据等腰三角形的腰的情况分类讨论即可;
(3)过点A作AB⊥x轴于B,设点A的坐标为(x,y),则OB·AB=x·y=12,根据等腰直角三角形的性质,可得:AB=MB=BN,然后根据平方差公式,即可求出ON-OM的值.
解:(1)∵点A在反比例函数y=![]() (x > 0)的图象上,AB⊥y轴
(x > 0)的图象上,AB⊥y轴
∴S△ABO=![]()
故答案为:6;
(2)将x=4代入y=![]() 中,得:y=3
中,得:y=3
∴点A的坐标为(4,3)
设点P的坐标为(a,0)由题意可知:a>0
∴OA=![]() ,OP=a,AP=
,OP=a,AP=![]()
①当OA=OP时,如下图所示
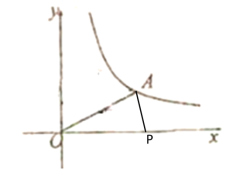
∴a=5
此时点P的坐标为(5,0);
②当OA=AP时,如下图所示
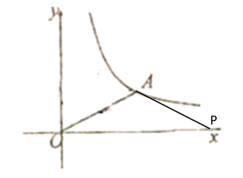
∴![]()
解得:![]() (不符合a的取值范围,舍去),
(不符合a的取值范围,舍去),
此时点P的坐标为(8,0);
③当OP=AP时,如下图所示
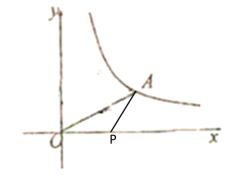
∴![]()
解得:![]()
此时点P的坐标为(![]() ,0).
,0).
综上所述:点P的坐标为(5,0)或(8,0)或(![]() ,0);
,0);
(3)如图所示,过点A作AB⊥x轴于B
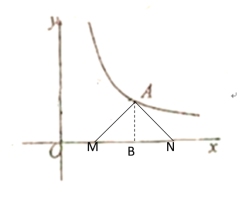
∴OB·AB=x·y=12
∵△AMN为等腰直角三角形,AB⊥x轴
∴AB=MB=BN
∴ON-OM
=(ON-OM)(ON+OM)
=MN(OB+BN+OB-BM)
=(MB+BN)(OB+BN+OB-BM)
=(AB + AB)(OB+ AB +OB- AB)
=2AB·2OB
=4AB·OB
=48


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
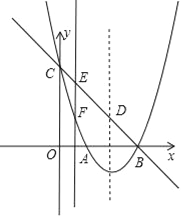
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AM为边BC上的中线,动点D在直线AM上,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
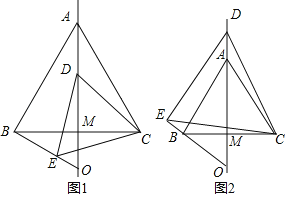
(1)如图1,点D在线段AM上时,填空:
①线段AD与BE的数量关系是 ②∠AOB的度数是 .
(2)如图2,当动点D在线段MA的延长线上时,试判断(1)中的结论是否成立?若成立,请给予证明:若不成立,请写出新的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子![]() 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=![]() 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=![]() (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
(销售利润=销售价-成本价)

查看答案和解析>>
科目:初中数学 来源: 题型:
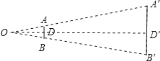
【题目】如图,数学趣闻:上世纪九十年代,国外有人传说:“从月亮上看地球,长城是肉眼唯一看得见的建筑物.”设长城的厚度为![]() ,人的正常视力能看清的最小物体所形成的视角为
,人的正常视力能看清的最小物体所形成的视角为![]() ,且已知月、地两球之间的距离为
,且已知月、地两球之间的距离为![]() ,根据学过的数学知识,你认为这个传说________.(请填“可能”或“不可能”,参考数据:
,根据学过的数学知识,你认为这个传说________.(请填“可能”或“不可能”,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
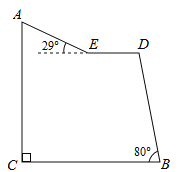
【题目】 “蘑菇石”是我省著名自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1790m.如图,DE∥BC,BD=1700m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com