
【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子![]() 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=![]() 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=![]() (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____.
科目:初中数学 来源: 题型:
【题目】如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是 .

A. ① ② B. ① ② ③ C. ③ ④ D. ① ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 94 | 86 | 90 |
学生乙 | 94 | 82 | 93 | 91 |
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是______.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2 ;依此类推,则∠P5=______.(用α、β表示)



查看答案和解析>>
科目:初中数学 来源: 题型:
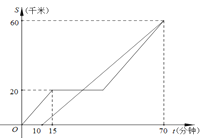
【题目】甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
(1)甲、乙两车行驶时的速度分别为多少?
(2)乙车出发多少分钟后第一次与甲车相遇?
(3)甲车中途因故障停止行驶的时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A在反比例函数y=![]() (x > 0)的图象上,作AB⊥y轴于B点.
(x > 0)的图象上,作AB⊥y轴于B点.
(1) △ABO的面积为 .
(2) 若点A的横坐标为4,点P在x轴的正半轴.且△OAP是等腰三角形,求点P的坐标: .
(3)动点M从原点出发,沿x轴的正方向运动,以MA为直角边,在MA的右侧作等腰Rt△MAN=90°,若在点M运动过程中,斜边MN始终在x轴上,求ON-OM的值
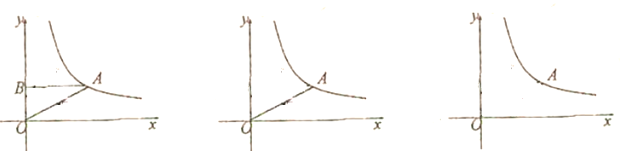
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图:已知A(﹣2,1),B(﹣1,2),C(﹣3,4).
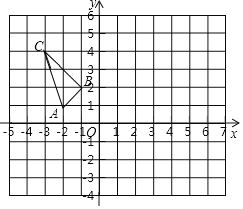
(1)画出与三角形ABC关于y轴对称的三角形A1B1C1;
(2)将三角形A1B1C1先向右平移2个单位,再向下平移1个单位,得到三角形A2B2C2,则三角形A2B2C2顶点坐标分别为:A2 B2 C2 ;
(3)若点P(a-1,b+2)与点A关于x轴对称,则a= ,b= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com