
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 94 | 86 | 90 |
学生乙 | 94 | 82 | 93 | 91 |
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
【答案】(1)甲的平均数90,甲方差8;乙的平均成绩90,乙的方差22.5;(2)甲的综合成绩90.4,乙的综合成绩89.6.
【解析】
(1)先计算出甲乙的平均成绩,再根据方差公式计算可得,继而由中位数的定义求解可得;
(2)根据加权平均数的定义计算可得.
解:(1)甲的平均数为![]() ×(90+94+86+90)=90(分),
×(90+94+86+90)=90(分),
则甲方差为![]() ×[(90﹣90)2×2+(94﹣90)2+(86﹣90)2]=8(分2);
×[(90﹣90)2×2+(94﹣90)2+(86﹣90)2]=8(分2);
乙的平均成绩为![]() ×(94+82+93+91)=90(分)
×(94+82+93+91)=90(分)
则乙的方差为![]() ×[(94﹣90)2+(82﹣90)2+(93﹣90)2+(91﹣90)2]=22.5(分2);
×[(94﹣90)2+(82﹣90)2+(93﹣90)2+(91﹣90)2]=22.5(分2);
(2)甲的综合成绩为![]() ×(90×3+94×3+86×2+90×2)=90.4(分),
×(90×3+94×3+86×2+90×2)=90.4(分),
乙的综合成绩为![]() ×(94×3+82×3+93×2+91×2)=89.6(分).
×(94×3+82×3+93×2+91×2)=89.6(分).


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
例:已知![]() ,
,![]() ,其中
,其中![]() ,求证:
,求证:![]() .
.
证明:![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(1)操作感知:比较大小:
①若![]() ,则
,则![]() ______
______![]() ;
;
②![]() ______
______![]() .
.
(2)类比探究:已知![]() ,
,![]() ,试运用上述方法比较
,试运用上述方法比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(3)应用拓展:已知![]() ,
,![]() 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论![]() 取何值,点
取何值,点![]() 始终在点
始终在点![]() 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AM为边BC上的中线,动点D在直线AM上,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
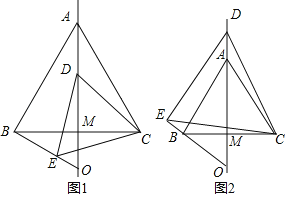
(1)如图1,点D在线段AM上时,填空:
①线段AD与BE的数量关系是 ②∠AOB的度数是 .
(2)如图2,当动点D在线段MA的延长线上时,试判断(1)中的结论是否成立?若成立,请给予证明:若不成立,请写出新的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y =ax2+bx+ c的图象如图,有以下结论:①a+b+c<0; ②a-b+c >2;③abc>0;④4a-2b+c <0;⑤c-a>1.其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子![]() 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=![]() 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=![]() (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )

A. 图象关于直线x=1对称 B. 函数y=ax2+bx+c(a≠0)的最小值是-![]()
C. -1和3是方程ax2+bx+c=0(a≠0)的两个根 D. 当x<1时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com