
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值

【答案】(1)证明见解析;(2)①证明见解析;②5.
【解析】
(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;
(2)①由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC;
②由△CBH∽△OBC可知:![]() ,所以HB=
,所以HB=![]() ,由于BC=HC,所以OH+HC=4
,由于BC=HC,所以OH+HC=4![]() +BC,利用二次函数的性质即可求出OH+HC的最大值.
+BC,利用二次函数的性质即可求出OH+HC的最大值.
(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线;
(2)①∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC
②由△CBH∽△OBC可知:![]()
∵AB=8,
∴BC2=HBOC=4HB,
∴HB=![]() ,
,
∴OH=OB-HB=4-![]()
∵CB=CH,
∴OH+HC=4![]() +BC,
+BC,
当∠BOC=90°,
此时BC=4![]()
∵∠BOC<90°,
∴0<BC<4![]() ,
,
令BC=x则CH=x,BH=![]()
![]()
当x=2时,
∴OH+HC可取得最大值,最大值为5


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,在边长为
,在边长为![]() 的小正方形组成的网格中,
的小正方形组成的网格中,![]() 的顶点
的顶点![]() 、
、![]() 均在格点上,点
均在格点上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .
.

![]() 点
点![]() 关于点
关于点![]() 中心对称的点的坐标为________;
中心对称的点的坐标为________;
![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到
后得到![]() ,那么点
,那么点![]() 的坐标为________;线段
的坐标为________;线段![]() 在旋转过程中所扫过的面积是________.
在旋转过程中所扫过的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是 .

A. ① ② B. ① ② ③ C. ③ ④ D. ① ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是点( )
个单位长度,则第2018秒时,点P的坐标是点( )

A. (2017,1) B. (2018,0) C. (2017,﹣1) D. (2019,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是等边△ABC内一点,连接PC,以PC为边作等边三角形△PDC,连接PA,PB,BD.
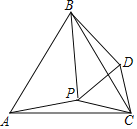
(1)求证:∠APC=∠BDC;
(2)当∠APC=150°时,试猜想△DPB的形状,并说明理由;
(3)当∠APB=100°且DB=PB,求∠APC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=6,AD=8,沿BD折叠使点A到点A′处,DA′交BC于点F.
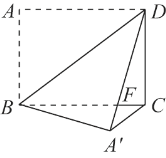
(1)求证:FB=FD;
(2)求证:CA′∥BD;
(3)求△DBF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 94 | 86 | 90 |
学生乙 | 94 | 82 | 93 | 91 |
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com