
【题目】如图所示,在平面直角坐标系中,半径均为1个单位的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是点( )
个单位长度,则第2018秒时,点P的坐标是点( )

A. (2017,1) B. (2018,0) C. (2017,﹣1) D. (2019,0)
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,点
是等边三角形,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,把
,把![]() 绕着点
绕着点![]() 按逆时针方向旋转,使边
按逆时针方向旋转,使边![]() 与
与![]() 重合,得到
重合,得到![]() ,连接
,连接![]() .求:
.求:![]() 的长及点
的长及点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
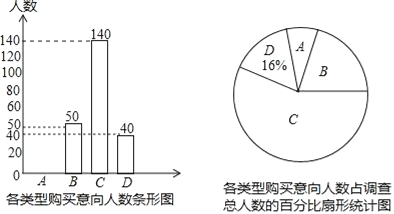
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
查看答案和解析>>
科目:初中数学 来源: 题型:
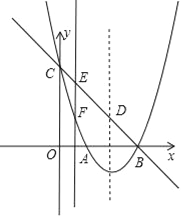
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至![]() ,旋转角为
,旋转角为![]() .
.

(1)当点![]() 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角![]() 的值;
的值;
(2)如图2,G为BC的中点,且00<![]() <900,求证:
<900,求证:![]() ;
;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,![]() 与
与![]() 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
例:已知![]() ,
,![]() ,其中
,其中![]() ,求证:
,求证:![]() .
.
证明:![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(1)操作感知:比较大小:
①若![]() ,则
,则![]() ______
______![]() ;
;
②![]() ______
______![]() .
.
(2)类比探究:已知![]() ,
,![]() ,试运用上述方法比较
,试运用上述方法比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(3)应用拓展:已知![]() ,
,![]() 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论![]() 取何值,点
取何值,点![]() 始终在点
始终在点![]() 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com