
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至![]() ,旋转角为
,旋转角为![]() .
.

(1)当点![]() 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角![]() 的值;
的值;
(2)如图2,G为BC的中点,且00<![]() <900,求证:
<900,求证:![]() ;
;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,![]() 与
与![]() 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
【答案】(1)∠α=300(2)见解析(3)旋转角a的值为1350或3150时,△BCD′与∠DCD′全等
【解析】
试题(1)根据旋转的性质得CE=CH=1,即可得出结论;
(2)由G为BC中点可得CG=CE,根据旋转的性质得∠D′CE′=∠DCE=90°,CE=CE′CE,则∠GCD′=∠DCE′=90°+α,然后根据“SAS”可判断△GCD′≌△E′CD,则GD′=E′D;
(3)根据正方形的性质得CB=CD,而CD=CD′,则△BCD′与△DCD′为腰相等的两等腰三角形,当两顶角相等时它们全等,当△BCD′与△DCD′为钝角三角形时,可计算出α=135°,当△BCD′与△DCD′为锐角三角形时,可计算得到α=315°.
试题解析:(1)
∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴CE=CH=1,∴△CEH为等腰直角三角形,∴∠ECH=45°,∴∠α=30°;
(2)证明:∵G为BC中点,∴CG=1,∴CG=CE,∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴∠D′CE′=∠DCE=90°,CE=CE′=CG,∴∠GCD′=∠DCE′=90°+α,在△GCD′和△E′CD中,∵CD′=CD,∠GCD=∠DCE′,CG=CE′,∴△GCD′≌△E′CD(SAS),∴GD′=E′D;
(3)解:能.
理由如下:
∵四边形ABCD为正方形,∴CB=CD,∵CD′=CD′,∴△BCD′与△DCD′为腰相等的两等腰三角形,当∠BCD′=∠DCD′时,△BCD′≌△DCD′,当△BCD′与△DCD′为钝角三角形时,则旋转角α=(360°-90°)÷2=135°,当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′=![]() ∠BCD=45°,则α=360°﹣90°÷2=315°,即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.
∠BCD=45°,则α=360°﹣90°÷2=315°,即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】节能环保的油电混合动力汽车,既可用油做动力行驶,也可用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求汽车行驶中每千米用电费用是多少元?
(2)甲、乙两地的距离是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
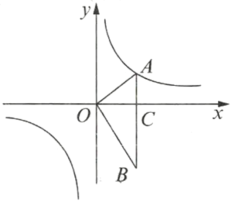
【题目】如图,在平面直角坐标系中,![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上.
的图像上.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求![]() 面积;
面积;
(3)在坐标轴上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,若存在,请直接写出所有符合条件的点
三点为顶点的三角形是等腰三角形,若存在,请直接写出所有符合条件的点![]() 的坐标;若不存在,简述你的理由.
的坐标;若不存在,简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克.若销售价每涨1元,则月销售量减少10千克.
(1)要使月销售利润达到最大,销售单价应定为多少元?
(2)要使月销售利润不低于8000元,请结合图象说明销售单价应如何定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是点( )
个单位长度,则第2018秒时,点P的坐标是点( )

A. (2017,1) B. (2018,0) C. (2017,﹣1) D. (2019,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=6,AD=8,沿BD折叠使点A到点A′处,DA′交BC于点F.
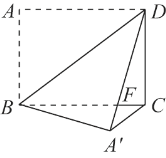
(1)求证:FB=FD;
(2)求证:CA′∥BD;
(3)求△DBF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,对角线
,对角线![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,若动点
,若动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒
秒![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
![]() 如图
如图![]() ,若点
,若点![]() 在对角线
在对角线![]() 上,
上,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 运动至点
运动至点![]() 止.设点
止.设点![]() 运动了
运动了![]() 秒,请你探索:从运动开始,经过多少时间,以点
秒,请你探索:从运动开始,经过多少时间,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?请求出所有可能的结果.
为顶点的三角形是等腰三角形?请求出所有可能的结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com