
【题目】如图,在长方形ABCD中,AB=6,AD=8,沿BD折叠使点A到点A′处,DA′交BC于点F.
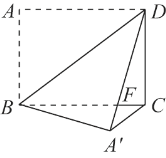
(1)求证:FB=FD;
(2)求证:CA′∥BD;
(3)求△DBF的面积.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据折叠的性质和矩形的性质可得∠ADB=∠BDA′,∠ADB=∠DBC,等量代换求出∠BDA′=∠DBC,然后根据等角对等边可得结论;
(2)首先求出FC=FA′,得到∠FCA′=∠FA′C,然后根据∠BFD=∠CFA′求出∠FBD=∠FCA′,利用平行线的判定可得结论;
(3)设FB=FD=x,则A′F=8-x,在Rt△BA′F中,利用勾股定理构造方程求出BF即可解决问题.
解:(1)由折叠的性质可得:∠ADB=∠BDA′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠BDA′=∠DBC,
∴FB=FD;
(2)由折叠的性质可得:AD=A′D,
∵四边形ABCD是矩形,
∴AD=BC,
∴A′D=BC,
∵FB=FD,
∴FC=FA′,
∴∠FCA′=∠FA′C,
∵∠BFD=∠CFA′,
∴∠FBD+∠FDB=∠FCA′+∠FA′C,即2∠FBD=2∠FCA′,
∴∠FBD=∠FCA′,
∴CA′∥BD;
(3)∵AD=A′D=8,AB=A′B=6,FB=FD,∠BA′F=∠A=90°,
∴设FB=FD=x,则A′F=8-x,
在Rt△BA′F中,∵BA′2+A′F2=BF2,
∴![]() ,
,
解得:![]() ,即
,即![]() ,
,
∴![]() .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
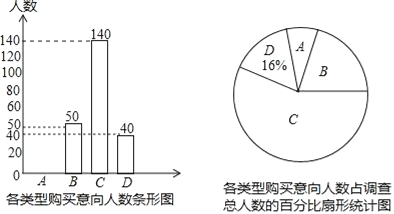
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至![]() ,旋转角为
,旋转角为![]() .
.

(1)当点![]() 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角![]() 的值;
的值;
(2)如图2,G为BC的中点,且00<![]() <900,求证:
<900,求证:![]() ;
;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,![]() 与
与![]() 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条长![]() 米,宽
米,宽![]() 米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为
米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为![]() 米2的
米2的![]() 个矩形小块,则小路的宽度应为( )
个矩形小块,则小路的宽度应为( )

A. ![]() 米或
米或![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
例:已知![]() ,
,![]() ,其中
,其中![]() ,求证:
,求证:![]() .
.
证明:![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(1)操作感知:比较大小:
①若![]() ,则
,则![]() ______
______![]() ;
;
②![]() ______
______![]() .
.
(2)类比探究:已知![]() ,
,![]() ,试运用上述方法比较
,试运用上述方法比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(3)应用拓展:已知![]() ,
,![]() 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论![]() 取何值,点
取何值,点![]() 始终在点
始终在点![]() 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y =ax2+bx+ c的图象如图,有以下结论:①a+b+c<0; ②a-b+c >2;③abc>0;④4a-2b+c <0;⑤c-a>1.其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在一条直线上,AB=DE,AB∥DE,∠A=∠D.

(1)求证:△ABC≌△DEF;(2)AC和DF存在怎样的关系?(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com