
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚΈ“Ο«÷ΣΒάΘ§±»ΫœΝΫ ΐΘ® ΫΘ©¥σ–Γ”–ΚήΕύΖΫΖ®Θ§ΓΑΉς≤νΖ®Γ± «≥Θ”ΟΒΡΖΫΖ®÷°“ΜΘ§Τδ‘≠άμ «≤ΜΒ» ΫΘ®ΜρΒ» ΫΘ©ΒΡ–‘÷ ΘΚ»τ![]() Θ§‘ρ
Θ§‘ρ![]() ΘΜ»τ
ΘΜ»τ![]() Θ§‘ρ
Θ§‘ρ![]() ΘΜ»τ
ΘΜ»τ![]() Θ§‘ρ
Θ§‘ρ![]() .
.
άΐΘΚ“―÷Σ![]() Θ§
Θ§![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() .
.
÷ΛΟςΘΚ![]()
![]() .
.
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ§Γύ
Θ§Γύ![]() .
.
Θ®1Θ©≤ΌΉςΗ–÷ΣΘΚ±»Ϋœ¥σ–ΓΘΚ
ΔΌ»τ![]() Θ§‘ρ
Θ§‘ρ![]() ______
______![]() ΘΜ
ΘΜ
ΔΎ![]() ______
______![]() .
.
Θ®2Θ©άύ±»ΧΫΨΩΘΚ“―÷Σ![]() Θ§
Θ§![]() Θ§ ‘‘Υ”Ο…œ ωΖΫΖ®±»Ϋœ
Θ§ ‘‘Υ”Ο…œ ωΖΫΖ®±»Ϋœ![]() ΓΔ
ΓΔ![]() ΒΡ¥σ–ΓΘ§≤ΔΥΒΟςάμ”….
ΒΡ¥σ–ΓΘ§≤ΔΥΒΟςάμ”….
Θ®3Θ©”Π”ΟΆΊ’ΙΘΚ“―÷Σ![]() Θ§
Θ§![]() ΈΣΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΒΡΝΫΒψΘ§–ΓΟς»œΈΣΘ§Έό¬έ
ΈΣΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΒΡΝΫΒψΘ§–ΓΟς»œΈΣΘ§Έό¬έ![]() »ΓΚΈ÷ΒΘ§Βψ
»ΓΚΈ÷ΒΘ§Βψ![]() Φ÷’‘ΎΒψ
Φ÷’‘ΎΒψ![]() ΒΡ…œΖΫΘ§–ΓΟςΒΡ≤¬œκΕ‘¬πΘΩΈΣ ≤Ο¥ΘΩ
ΒΡ…œΖΫΘ§–ΓΟςΒΡ≤¬œκΕ‘¬πΘΩΈΣ ≤Ο¥ΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ![]() Θ§ΔΎ
Θ§ΔΎ![]() ;(2)M<NΘ§άμ”…ΦϊΫβΈωΘΜΘ®3Θ©–ΓΟςΒΡ≤¬œκ «Ε‘ΒΡΘ§άμ”…ΦϊΫβΈω
;(2)M<NΘ§άμ”…ΦϊΫβΈωΘΜΘ®3Θ©–ΓΟςΒΡ≤¬œκ «Ε‘ΒΡΘ§άμ”…ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΗυΨί≤ΜΒ» ΫΒΡ–‘÷ Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜΔΎΗυΨίΆξ»ΪΤΫΖΫΙΪ ΫΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ®2Θ©ΝΫ ΫœύΦθΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ®3Θ©ΝΫΒψΚαΉχ±ξœύΆ§Θ§±»ΫœΉίΉχ±ξΒΡ¥σ–ΓΦ¥Ω…ΒΟ≥ω¥πΑΗ.
Θ®1Θ©ΔΌΓΏ![]()
Γύa+b<0Θ§a-b<0
Γύ![]() <0
<0
Ι ¥πΑΗΈΣΘΚ<.
ΔΎ![]()
Ι ¥πΑΗΈΣΘΚΓί.
Θ®2Θ©![]() Θ§άμ”…ΘΚ…η
Θ§άμ”…ΘΚ…η![]() Θ§
Θ§
‘ρ![]()
![]() Θ§
Θ§
Γύ![]() .
.
Θ®3Θ©–ΓΟςΒΡ≤¬œκ «Ε‘ΒΡΘ§άμ”…»γœ¬ΘΚ![]() Θ§
Θ§
Υυ“‘Θ§Έό¬έ![]() »ΓΚΈ÷ΒΘ§Βψ
»ΓΚΈ÷ΒΘ§Βψ![]() ΕΦ‘ΎΒψ
ΕΦ‘ΎΒψ![]() ΒΡ…œΖΫΘ§Φ¥–ΓΟςΒΡΙέΒψ’ΐ»Ζ.
ΒΡ…œΖΫΘ§Φ¥–ΓΟςΒΡΙέΒψ’ΐ»Ζ.


 Οϊ ΠΒΦΚΫΒΞ‘ΣΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
Οϊ ΠΒΦΚΫΒΞ‘ΣΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ Οϊ–ΘΟϊΨμΒΞ‘ΣΆ§≤Ϋ―ΒΝΖ≤β ‘ΧβœΒΝ–¥πΑΗ
Οϊ–ΘΟϊΨμΒΞ‘ΣΆ§≤Ϋ―ΒΝΖ≤β ‘ΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§―ρΡξ¥ΚΫΎΒΫΝΥΘ§–ΓΟς«Ή ÷÷ΤΉςΝΥ![]() ’≈“Μ―υΒΡΩ®Τ§Θ§‘ΎΟΩ’≈Ω®Τ§…œΖ÷±π–¥…œΓΑ–¬Γ±ΓΑΡξΓ±ΓΑΚΟΓ±»ΐΗωΉ÷Θ§≤ΔΥφΜζΖ≈»κ“ΜΗω≤ΜΆΗΟςΒΡ–≈Ζβ÷–Θ§»ΜΚσ»Ο–ΓΖΦΖ÷»ΐ¥Έ¥”–≈Ζβ÷–Οΰ
’≈“Μ―υΒΡΩ®Τ§Θ§‘ΎΟΩ’≈Ω®Τ§…œΖ÷±π–¥…œΓΑ–¬Γ±ΓΑΡξΓ±ΓΑΚΟΓ±»ΐΗωΉ÷Θ§≤ΔΥφΜζΖ≈»κ“ΜΗω≤ΜΆΗΟςΒΡ–≈Ζβ÷–Θ§»ΜΚσ»Ο–ΓΖΦΖ÷»ΐ¥Έ¥”–≈Ζβ÷–Οΰ![]() ’≈Ω®Τ§Θ®ΟΩ¥ΈΟΰ
’≈Ω®Τ§Θ®ΟΩ¥ΈΟΰ![]() ’≈Θ§Οΰ≥ω≤ΜΖ≈ΜΊΘ©Θ°
’≈Θ§Οΰ≥ω≤ΜΖ≈ΜΊΘ©Θ°
![]()
![]() –ΓΖΦΒΎ“Μ¥Έ≥ι»ΓΒΡΩ®Τ§ «ΓΑ–¬Γ±Ή÷ΒΡΗ≈¬ «Εύ…ΌΘΩ
–ΓΖΦΒΎ“Μ¥Έ≥ι»ΓΒΡΩ®Τ§ «ΓΑ–¬Γ±Ή÷ΒΡΗ≈¬ «Εύ…ΌΘΩ
![]() «κΆ®ΙΐΜ≠ ςΉ¥ΆΦΜρΝ–±μΘ§«σ–ΓΖΦœ»Κσ≥ι»ΓΒΡ
«κΆ®ΙΐΜ≠ ςΉ¥ΆΦΜρΝ–±μΘ§«σ–ΓΖΦœ»Κσ≥ι»ΓΒΡ![]() ’≈Ω®Τ§Ζ÷±π «ΓΑ–¬ΡξΚΟΓ±ΒΡΗ≈¬ Θ°
’≈Ω®Τ§Ζ÷±π «ΓΑ–¬ΡξΚΟΓ±ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΑκΨΕΨυΈΣ1ΗωΒΞΈΜΒΡΑκ‘≤O1Θ§O2Θ§O3Θ§Γ≠Ήι≥…“ΜΧθΤΫΜ§ΒΡ«ζœΏΘ§ΒψP¥”‘≠ΒψO≥ωΖΔΘ§―Ί’βΧθ«ζœΏœρ”“‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§‘ρΒΎ2018Οκ ±Θ§ΒψPΒΡΉχ±ξ «ΒψΘ®ΓΓΓΓΘ©
ΗωΒΞΈΜ≥ΛΕ»Θ§‘ρΒΎ2018Οκ ±Θ§ΒψPΒΡΉχ±ξ «ΒψΘ®ΓΓΓΓΘ©

A. Θ®2017Θ§1Θ© B. Θ®2018Θ§0Θ© C. Θ®2017Θ§©¹1Θ© D. Θ®2019Θ§0Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ≥ΛΖΫ–ΈABCD÷–Θ§ABΘΫ6Θ§ADΘΫ8Θ§―ΊBD’έΒΰ ΙΒψAΒΫΒψAΓδ¥ΠΘ§DAΓδΫΜBC”ΎΒψF.
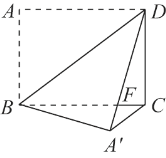
(1)«σ÷ΛΘΚFBΘΫFDΘΜ
(2)«σ÷ΛΘΚCAΓδΓΈBDΘΜ
(3)«σΓςDBFΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΆχΒξœζ έΦΉΓΔ““ΝΫ÷÷”πΟΪ«ρΘ§“―÷ΣΦΉ÷÷”πΟΪ«ρΟΩΆ≤ΒΡ έΦέ±»““÷÷”πΟΪ«ρΕύ15‘ΣΘ§Άθάœ Π¥”ΗΟΆχΒξΙΚ¬ρΝΥ2Ά≤ΦΉ÷÷”πΟΪ«ρΚΆ3Ά≤““÷÷”πΟΪ«ρΘ§Ι≤Μ®Ζ―255‘ΣΘ°
Θ®1Θ©ΗΟΆχΒξΦΉΓΔ““ΝΫ÷÷”πΟΪ«ρΟΩΆ≤ΒΡ έΦέΗς «Εύ…Ό‘ΣΘΩ
Θ®2Θ©ΗυΨίœϊΖ―’Ώ–η«σΘ§ΗΟΆχΒξΨωΕ®”Ο≤Μ≥§Ιΐ8780‘ΣΙΚΫχΦΉΓΔ““ΝΫ÷÷”πΟΪ«ρΙ≤200Ά≤Θ§«“ΦΉ÷÷”πΟΪ«ρΒΡ ΐΝΩ¥σ”Ύ““÷÷”πΟΪ«ρ ΐΝΩΒΡ![]() Θ§“―÷ΣΦΉ÷÷”πΟΪ«ρΟΩΆ≤ΒΡΫχΦέΈΣ50‘ΣΘ§““÷÷”πΟΪ«ρΟΩΆ≤ΒΡΫχΦέΈΣ40‘ΣΘ°
Θ§“―÷ΣΦΉ÷÷”πΟΪ«ρΟΩΆ≤ΒΡΫχΦέΈΣ50‘ΣΘ§““÷÷”πΟΪ«ρΟΩΆ≤ΒΡΫχΦέΈΣ40‘ΣΘ°
ΔΌ»τ…ηΙΚΫχΦΉ÷÷”πΟΪ«ρmΆ≤Θ§‘ρΗΟΆχΒξ”–ΡΡΦΗ÷÷ΫχΜθΖΫΑΗΘΩ
ΔΎ»τΥυΙΚΫχ”πΟΪ«ρΨυΩ…»Ϊ≤Ω έ≥ωΘ§«κ«σ≥ωΆχΒξΥυΜώάϊ»σWΘ®‘ΣΘ©”κΦΉ÷÷”πΟΪ«ρΫχΜθΝΩmΘ®Ά≤Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤ΔΥΒΟςΒ±mΈΣΚΈ÷Β ±ΥυΜώάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§«“
Θ§«“![]() Θ§
Θ§![]() Θ§Ε‘Ϋ«œΏ
Θ§Ε‘Ϋ«œΏ![]() Θ°
Θ°
![]() «σ÷ΛΘΚΥΡ±Ώ–Έ
«σ÷ΛΘΚΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘΜ
«ΨΊ–ΈΘΜ
![]() »γΆΦ
»γΆΦ![]() Θ§»τΕ·Βψ
Θ§»τΕ·Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§‘Ύ
≥ωΖΔΘ§‘Ύ![]() ±Ώ…œ“‘ΟΩΟκ
±Ώ…œ“‘ΟΩΟκ![]() ΒΡΥΌΕ»œρΒψ
ΒΡΥΌΕ»œρΒψ![]() ‘»ΥΌ‘ΥΕ·Θ§Ά§ ±Ε·Βψ
‘»ΥΌ‘ΥΕ·Θ§Ά§ ±Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§‘Ύ
≥ωΖΔΘ§‘Ύ![]() ±Ώ…œ“‘ΟΩΟκ
±Ώ…œ“‘ΟΩΟκ![]() ΒΡΥΌΕ»œρΒψ
ΒΡΥΌΕ»œρΒψ![]() ‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣ
‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣ![]() Οκ
Οκ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§»τ
Θ§»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
![]() »γΆΦ
»γΆΦ![]() Θ§»τΒψ
Θ§»τΒψ![]() ‘ΎΕ‘Ϋ«œΏ
‘ΎΕ‘Ϋ«œΏ![]() …œΘ§
…œΘ§![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ¥”
¥”![]() Βψ≥ωΖΔΘ§“‘ΟΩΟκ
Βψ≥ωΖΔΘ§“‘ΟΩΟκ![]() ΒΡΥΌΕ»―Ί
ΒΡΥΌΕ»―Ί![]() ‘ΥΕ·÷ΝΒψ
‘ΥΕ·÷ΝΒψ![]() ÷ΙΘ°…ηΒψ
÷ΙΘ°…ηΒψ![]() ‘ΥΕ·ΝΥ
‘ΥΕ·ΝΥ![]() ΟκΘ§«κΡψΧΫΥςΘΚ¥”‘ΥΕ·ΩΣ ΦΘ§Ψ≠ΙΐΕύ…Ό ±ΦδΘ§“‘Βψ
ΟκΘ§«κΡψΧΫΥςΘΚ¥”‘ΥΕ·ΩΣ ΦΘ§Ψ≠ΙΐΕύ…Ό ±ΦδΘ§“‘Βψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘΩ«κ«σ≥ωΥυ”–Ω…ΡήΒΡΫαΙϊΘ°
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘΩ«κ«σ≥ωΥυ”–Ω…ΡήΒΡΫαΙϊΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΈΜΆ§―ß≤ΈΦ” ΐ―ßΉέΚœΥΊ÷ ≤β ‘Θ§Ηςœν≥…Φ®»γœ¬Θ®ΒΞΈΜΘΚΖ÷Θ©
ΐ”κ¥ζ ΐ | Ω’Φδ”κΆΦ–Έ | Ά≥ΦΤ”κΗ≈¬ | ΉέΚœ”κ ΒΦυ | |
―ß…ζΦΉ | 90 | 94 | 86 | 90 |
―ß…ζ““ | 94 | 82 | 93 | 91 |
Θ®1Θ©Ζ÷±πΦΤΥψΦΉΓΔ““≥…Φ®ΒΡΤΫΨυ ΐΚΆΖΫ≤νΘΜ
Θ®2Θ©»γΙϊ ΐ”κ¥ζ ΐΓΔΩ’Φδ”κΆΦ–ΈΓΔΆ≥ΦΤ”κΗ≈¬ ΓΔΉέΚœ”κ ΒΦυΒΡ≥…Φ®Α¥3ΘΚ3ΘΚ2ΘΚ2ΦΤΥψΘ§Ρ«Ο¥ΦΉΓΔ““ΒΡ ΐ―ßΉέΚœΥΊ÷ ≥…Φ®Ζ÷±πΈΣΕύ…ΌΖ÷ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
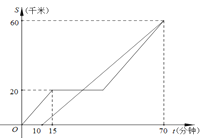
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ≥ΒΕΦ¥”AΒΊ«ΑΆυBΒΊΘ§»γΆΦΖ÷±π±μ ΨΦΉΓΔ““ΝΫ≥ΒάκAΒΊΒΡΨύάκSΘ®«ßΟΉΘ©”κ ±ΦδtΘ®Ζ÷÷”Θ©ΒΡΚ· ΐΙΊœΒ.“―÷ΣΦΉ≥Β≥ωΖΔ10Ζ÷÷”Κσ““≥Β≤≈≥ωΖΔΘ§ΦΉ≥Β÷–ΆΨ“ρΙ ΆΘ÷Ι–– Μ“ΜΕΈ ±ΦδΚσΑ¥‘≠ΥΌΦΧ–χ ΜœρBΒΊΘ§Ήν÷’ΦΉΓΔ““ΝΫ≥ΒΆ§ ±ΒΫ¥οBΒΊΘ§ΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΦΉΓΔ““ΝΫ≥Β–– Μ ±ΒΡΥΌΕ»Ζ÷±πΈΣΕύ…ΌΘΩ
Θ®2Θ©““≥Β≥ωΖΔΕύ…ΌΖ÷÷”ΚσΒΎ“Μ¥Έ”κΦΉ≥Βœύ”ωΘΩ
Θ®3Θ©ΦΉ≥Β÷–ΆΨ“ρΙ ’œΆΘ÷Ι–– ΜΒΡ ±ΦδΈΣΕύ…ΌΖ÷÷”ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ“ΜΗω’ΐ±»άΐΚ· ΐΆΦœσyΘΫ2xΚΆ“ΜΗω“Μ¥ΈΚ· ΐyΘΫkx+bΒΡΆΦœσΫΜ”ΎΒψPΘ®©¹2Θ§aΘ©«““Μ¥ΈΚ· ΐΒΡΆΦœσ”κy÷αΒΡΫΜΒψQΒΡΉίΉχ±ξΈΣ4Θ°
Θ®1Θ©«σ’βΝΫΗωΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©‘ΎΆ§“ΜΉχ±ξœΒ÷–Θ§Ζ÷±πΜ≠≥ω’βΝΫΗωΚ· ΐΒΡΆΦœσΘΜ
Θ®3Θ©«σΓςPQOΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com