
【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,对角线
,对角线![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,若动点
,若动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒
秒![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
![]() 如图
如图![]() ,若点
,若点![]() 在对角线
在对角线![]() 上,
上,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 运动至点
运动至点![]() 止.设点
止.设点![]() 运动了
运动了![]() 秒,请你探索:从运动开始,经过多少时间,以点
秒,请你探索:从运动开始,经过多少时间,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?请求出所有可能的结果.
为顶点的三角形是等腰三角形?请求出所有可能的结果.

【答案】(1)详见解析;(2)![]() ;(3)从运动开始,经过
;(3)从运动开始,经过![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.
【解析】
(1)先判定四边形ABCD是平行四边形,再根据∠B=90°,得出四边形ABCD是矩形;
(2)先过Q作QM⊥BC于M点,AP与BQ交于点N,判定△ABP∽△BMQ,得出![]() =
=![]() ,即
,即![]() =
=![]() ,求得t的值即可;
,求得t的值即可;
(3)分为三种情况讨论:当CQ=CP=4cm时,当PQ=CQ=4cm时,当QP=CP时,分别根据等腰三角形的性质,求得BP的长,进而得到t的值.
![]() 证明:∵
证明:∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形;
是矩形;
![]() 如图,过
如图,过![]() 作
作![]() 于
于![]() 点,
点,![]() 与
与![]() 交于点
交于点![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
![]() 分为三种情况:
分为三种情况:
①如图![]() 所示,当
所示,当![]() 时,
时,![]() ,
,

∴![]() 秒;
秒;
②如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∵![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() 秒;
秒;
③如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
![]() ,
,![]() ,
,
∵![]() ,
,

∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 秒.
秒.
综上所述,从运动开始,经过![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】请从以下两题中任选一题作答,若多选,则按所选的第一题计分.
![]() 如图所示的四边形中,若去掉一个
如图所示的四边形中,若去掉一个![]() 的角得到一个五边形,则
的角得到一个五边形,则![]() ________.
________.
![]() 如果某人沿坡度
如果某人沿坡度![]() 的斜坡前进
的斜坡前进![]() ,那么他所在的位置比原来的位置升高了________
,那么他所在的位置比原来的位置升高了________![]() .(结果精确到
.(结果精确到![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至![]() ,旋转角为
,旋转角为![]() .
.

(1)当点![]() 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角![]() 的值;
的值;
(2)如图2,G为BC的中点,且00<![]() <900,求证:
<900,求证:![]() ;
;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,![]() 与
与![]() 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条长![]() 米,宽
米,宽![]() 米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为
米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为![]() 米2的
米2的![]() 个矩形小块,则小路的宽度应为( )
个矩形小块,则小路的宽度应为( )

A. ![]() 米或
米或![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
例:已知![]() ,
,![]() ,其中
,其中![]() ,求证:
,求证:![]() .
.
证明:![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(1)操作感知:比较大小:
①若![]() ,则
,则![]() ______
______![]() ;
;
②![]() ______
______![]() .
.
(2)类比探究:已知![]() ,
,![]() ,试运用上述方法比较
,试运用上述方法比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(3)应用拓展:已知![]() ,
,![]() 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论![]() 取何值,点
取何值,点![]() 始终在点
始终在点![]() 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
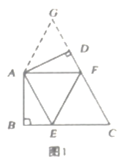
【题目】(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,探究图中
,探究图中![]() 之间的数量关系。小明同学探究此问题的方法是:延长
之间的数量关系。小明同学探究此问题的方法是:延长![]() 到点
到点![]() ,使
,使![]() 。连接
。连接![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,可得出结论。他的结论应是______________________________________(不写过程)。
,可得出结论。他的结论应是______________________________________(不写过程)。
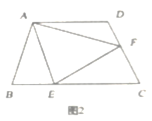
(2)如图2,若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由。
,上述结论是否仍然成立,并说明理由。
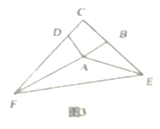
(3)如图3,已知在四边形![]() 中,
中,![]() ,
,![]() ,若点
,若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,仍然满足
的延长线上,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程。
的数量关系,并给出证明过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y =ax2+bx+ c的图象如图,有以下结论:①a+b+c<0; ②a-b+c >2;③abc>0;④4a-2b+c <0;⑤c-a>1.其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com