
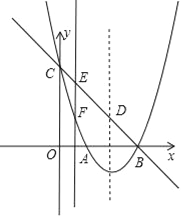
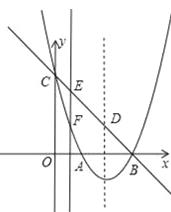
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
【答案】(1)抛物线解析式为y=x2﹣4x+3;(2)S△ACD=2;(3)存在满足条件的点E,其坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() )或(1,2)或(4,﹣1).
)或(1,2)或(4,﹣1).
【解析】试题分析:(1)设顶点式y=a(x-2)2-1(a≠0),然后把C点坐标代入求出a即可;
(2)通过解方程x2-4x+3=0得A(1,0),B(3,0),再利用待定系数法求出直线BC解析式为y=-x+3,从而得到D(2,1),然后利用S△ACD=S△ABC-S△ABD进行计算即可;
(3)易得∠FED≠90°,则△DEF为直角三角形,分∠DFE=90°和∠EDF=90°两种情况,①当∠DFE=90°时F点纵坐标为1,解方程x2-4x+3=1得点E的横坐标为2±![]() ,再利用点E在直线y=-x+3上可确定E点坐标;②当∠EDF=90°时,先确定直线AD解析式为y=x-1,则可判断AD⊥BC,所以直线AD与抛物线的交点即为E点,解方程x2-4x+3=x-1得E点的横坐标,然后利用直线BC的解析式确定E点坐标.
,再利用点E在直线y=-x+3上可确定E点坐标;②当∠EDF=90°时,先确定直线AD解析式为y=x-1,则可判断AD⊥BC,所以直线AD与抛物线的交点即为E点,解方程x2-4x+3=x-1得E点的横坐标,然后利用直线BC的解析式确定E点坐标.
(1)∵抛物线的顶点坐标为(2,﹣1),
∴可设抛物线解析式为y=a(x﹣2)2﹣1(a≠0),
把C(0,3)代入可得a(0﹣2)2﹣1=3,解得a=1,
∴抛物线解析式为y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(2)在y=x2﹣4x+3中,令y=0可得x2﹣4x+3=0,解得x=1或x=3,
∴A(1,0),B(3,0),
设直线BC解析式为y=kx+3,把B(3,0)代入得:3k+3=0,解得k=﹣1,
∴直线BC解析式为y=﹣x+3,
由(1)可知抛物线的对称轴为x=2,此时y=﹣x+3=1,
∴D(2,1),
∴S△ACD=S△ABC﹣S△ABD=![]() ×2×3﹣
×2×3﹣![]() ×2×1=2;
×2×1=2;
(3)由题意知EF∥y轴,则∠FED=∠OCB≠90°,
∴△DEF为直角三角形,分∠DFE=90°和∠EDF=90°两种情况,
①当∠DFE=90°时,即DF∥x轴,则D、F的纵坐标相同,
∴F点纵坐标为1,
∵点F在抛物线上,
∴x2﹣4x+3=1,解得x=2±![]() ,即点E的横坐标为2±
,即点E的横坐标为2±![]() ,
,
∵点E在直线y=﹣x+3上,
∴当x=2+![]() 时,y=﹣x+3=1﹣
时,y=﹣x+3=1﹣![]() ;
;
当x=2﹣![]() 时,y=﹣x+3=1+
时,y=﹣x+3=1+![]() ,
,
∴E点坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() );
);
②当∠EDF=90°时,
∵A(1,0),D(2,1),
∴直线AD解析式为y=x﹣1,
∵直线BC解析式为y=﹣x+3,
∴AD⊥BC,
∴直线AD与抛物线的交点即为E点,
联立直线AD与抛物线解析式有x2﹣4x+3=x﹣1,解得x=1或x=4,
当x=1时,y=﹣x+3=2;当x=4时,y=﹣x+3=﹣1,
∴E点坐标为(1,2)或(4,﹣1),
综上所述,存在满足条件的点E,其坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() )或(1,2)或(4,﹣1).
)或(1,2)或(4,﹣1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
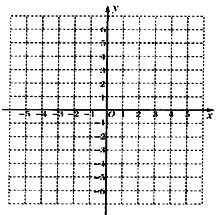
【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,
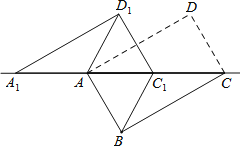
(1)求证:△A1AD1≌△CC1B;
(2)当CC1=1时,求证:四边形ABC1D1是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() .其中正确的个数是( )
.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() 垂足为
垂足为![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
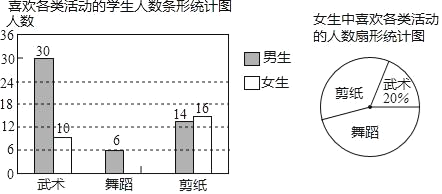
【题目】某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;
(4)已知该校有1200名学生,请结合数据简要分析该校学生对三项活动课程的兴趣情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com