
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() 垂足为
垂足为![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
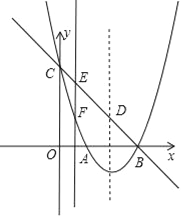
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 不平行,
不平行,![]() .
.![]() 为四边形
为四边形![]() 的对角线,
的对角线,![]()
![]() 分别是
分别是![]() 的中点下列结论:①
的中点下列结论:①![]() ;②四边形
;②四边形![]() 是矩形;③
是矩形;③![]() 平分
平分![]() ④
④![]() ;⑤四边形
;⑤四边形![]() 是菱形.其中正确的个数是 ( )
是菱形.其中正确的个数是 ( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点坐标为(3,3),将△ABC 先向下平移4个单位得△A'B'C',再将△A'B'C'绕点O逆时针旋转180°得△A'B'C'.
(1)请你画出△A'B'C'和△A'B'C';
(2)点A'的坐标为 ;
(3)△ABC和△A'B'C'关于某个点中心对称,这个点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的中线.

(1)利用尺规按下列要求作图,并在图中标明相应字母.(保留作图痕迹,不写作法)
①作线段AC的垂直平分线,分别交AC、AD、AB于点E、M、F;②连接CM、BM;
(2)若∠CAD=20°,求∠MCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是轴对称图形,且直线AC是否对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是( )

A. ①②③ B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学用一副扑克牌中牌面数字分别是:3,4,5,6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com