
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,
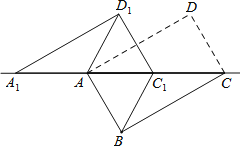
(1)求证:△A1AD1≌△CC1B;
(2)当CC1=1时,求证:四边形ABC1D1是菱形。
【答案】证明见解析
【解析】试题分析:(1)由矩形的性质及平移的性质易得∠A1=∠DAC,A1D1=AD,AA1=CC1,即可得到结论;
(2)由所给条件可证明△AC1B是等边三角形,即可得到ABC1D1是菱形.
试题解析:解:(1)∵四边形ABCD为矩形,
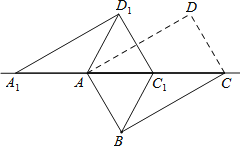
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠AA1 D1=∠DAC,A1D1=AD,AA1=CC1,
∴∠AA1 D1=∠ACB, BC= A1D1
在△A1AD1与△CC1B中,
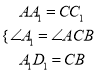 ,
,
∴△A1AD1≌△CC1B;
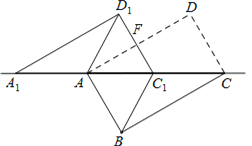
(2)证明∵∠ACB=30°,∴∠CAB=60°.
∵AB=1,∴AC=2.
∵CC1=1,∴AC1=1,∴△AC1B是等边三角形,.
∵AB=CD,CD=C1D1,∴AB= C1D1,∴四边形ABC1D1是平行四边形.
又AB=BC1,∴四边形ABC1D1是菱形.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.

(1)求证:DC=BE;
(2)若∠AEC=69°,求∠EDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别,某校模仿二维码建立了一个七年级学生身份识别系统,图2是七年级某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20+1.如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20+1=6表示该生为6班学生.则该系统最多能识别七年级的班级数是___个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
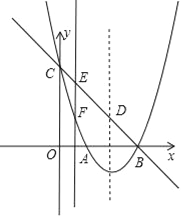
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建生态文明建设城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,甲队单独完成这项工程,刚好如期完成,每施工一天,需付工程款1.5万元;乙工程队单独完成这项工程要比规定工期多用a天,乙工程队每施工一天需付工程款1万元.若先由甲、乙两队一起合作b天,剩下的工程由乙队单独做,也正好如期完工
(1)当a=6,b=4时,求工程预定工期的天数.
(2)若a﹣b=2.a是偶数
①求甲队、乙队单独完成工期的天数(用含a的代数式表示)
②工程领导小组有三种施工方案:
方案一:甲队单独完成这项工程;
方案二:乙队单独完成这项工程;
方案三:先由甲、乙两队一起合作b天,剩下的工程由乙队单独做.
为了节省工程款,同时又能如期完工,请你选择一种方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 不平行,
不平行,![]() .
.![]() 为四边形
为四边形![]() 的对角线,
的对角线,![]()
![]() 分别是
分别是![]() 的中点下列结论:①
的中点下列结论:①![]() ;②四边形
;②四边形![]() 是矩形;③
是矩形;③![]() 平分
平分![]() ④
④![]() ;⑤四边形
;⑤四边形![]() 是菱形.其中正确的个数是 ( )
是菱形.其中正确的个数是 ( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的中线.

(1)利用尺规按下列要求作图,并在图中标明相应字母.(保留作图痕迹,不写作法)
①作线段AC的垂直平分线,分别交AC、AD、AB于点E、M、F;②连接CM、BM;
(2)若∠CAD=20°,求∠MCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
![]() ;
; ![]() ;
; ![]() ;
;
(3)求出△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com