
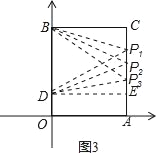
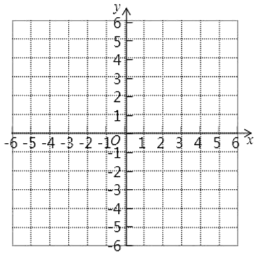
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌГЄЗНаЮOACBЕФЖЅЕуAЁЂBЗжБ№дкxжсгыyжсЩЯЃЌвбжЊOA=6ЃЌOB=10ЃЎЕуDЮЊyжсЩЯвЛЕуЃЌЦфзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛЕФЫйЖШбиЯпЖЮACЉCBЕФЗНЯђдЫЖЏЃЌЕБЕуPгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЎ
(1)ЕБЕуPОЙ§ЕуCЪБЃЌЧѓжБЯпDPЕФКЏЪ§НтЮіЪНЃЛ
(2)ЂйЧѓЁїOPDЕФУцЛ§SЙигкtЕФКЏЪ§НтЮіЪНЃЛ
ЂкШчЭМЂкЃЌАбГЄЗНаЮбизХOPелЕўЃЌЕуBЕФЖдгІЕуBЁфЧЁКУТфдкACБпЩЯЃЌЧѓЕуPЕФзјБъЃЎ
(3)ЕуPдкдЫЖЏЙ§ГЬжаЪЧЗёДцдкЪЙЁїBDPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ



ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x+2ЃЛЃЈ2ЃЉЂйSЃН6ЛђSЃНЉ2t+16ЃЛЂкЕуPЕФзјБъЪЧЃЈ
x+2ЃЛЃЈ2ЃЉЂйSЃН6ЛђSЃНЉ2t+16ЃЛЂкЕуPЕФзјБъЪЧЃЈ![]() ЃЌ10ЃЉЃЛЃЈ3ЃЉДцдкЃЌТњзуЬтвтЕФPзјБъЮЊЃЈ6ЃЌ6ЃЉЛђЃЈ6ЃЌ2
ЃЌ10ЃЉЃЛЃЈ3ЃЉДцдкЃЌТњзуЬтвтЕФPзјБъЮЊЃЈ6ЃЌ6ЃЉЛђЃЈ6ЃЌ2![]() +2ЃЉЛђЃЈ6ЃЌ10Љ2
+2ЃЉЛђЃЈ6ЃЌ10Љ2![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшжБЯпDPНтЮіЪНЮЊy=kx+bЃЌНЋDгыCзјБъДњШыЧѓГіkгыbЕФжЕЃЌМДПЩШЗЖЈГіНтЮіЪНЃЛ
ЃЈ2ЃЉЂйЕБPдкACЖЮЪБЃЌЁїODPЕзODгыИпЮЊЙЬЖЈжЕЃЌЧѓГіДЫЪБУцЛ§ЃЛЕБPдкBCЖЮЪБЃЌЕзБпODЮЊЙЬЖЈжЕЃЌБэЪОГіИпЃЌМДПЩСаГіSгыtЕФЙиЯЕЪНЃЛ
ЂкЕБDЙигкOPЕФЖдГЦЕуТфдкxжсЩЯЪБЃЌжБЯпOPЮЊy=xЃЌЧѓГіДЫЪБPзјБъМДПЩЃЛ
ЃЈ3ЃЉДцдкЃЌЗжБ№вдBDЃЌDPЃЌBPЮЊЕзБпШ§жжЧщПіПМТЧЃЌРћгУЙДЙЩЖЈРэМАЭМаЮгызјБъаджЪЧѓГіPзјБъМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпOAЃН6ЃЌOBЃН10ЃЌЫФБпаЮOACBЮЊГЄЗНаЮЃЌ
ЁрCЃЈ6ЃЌ10ЃЉЃЎ
ЩшДЫЪБжБЯпDPНтЮіЪНЮЊyЃНkx+bЃЌ
АбЃЈ0ЃЌ2ЃЉЃЌCЃЈ6ЃЌ10ЃЉЗжБ№ДњШыЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]()
дђДЫЪБжБЯпDPНтЮіЪНЮЊyЃН![]() x+2ЃЛ
x+2ЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкЯпЖЮACЩЯЪБЃЌODЃН2ЃЌИпЮЊ6ЃЌSЃН6ЃЛ
ЕБЕуPдкЯпЖЮBCЩЯЪБЃЌODЃН2ЃЌИпЮЊ6+10Љ2tЃН16Љ2tЃЌSЃН![]() ЁС2ЁСЃЈ16Љ2tЃЉЃНЉ2t+16ЃЛ
ЁС2ЁСЃЈ16Љ2tЃЉЃНЉ2t+16ЃЛ
ЂкЩшPЃЈmЃЌ10ЃЉЃЌдђPBЃНPBЁфЃНmЃЌШчЭМ2ЃЌ
ЁпOBЁфЃНOBЃН10ЃЌOAЃН6ЃЌ
ЁрABЁфЃН![]() ЃН8ЃЌ
ЃН8ЃЌ
ЁрBЁфCЃН10Љ8ЃН2ЃЌ
ЁпPCЃН6ЉmЃЌ
Ёрm2ЃН22+ЃЈ6ЉmЃЉ2ЃЌНтЕУmЃН![]()
дђДЫЪБЕуPЕФзјБъЪЧЃЈ![]() ЃЌ10ЃЉЃЛ
ЃЌ10ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩЮЊЃК
ШєЁїBDPЮЊЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіПМТЧЃКШчЭМ3ЃЌ
ЂйЕБBDЃНBP1ЃНOBЉODЃН10Љ2ЃН8ЃЌ
дкRtЁїBCP1жаЃЌBP1ЃН8ЃЌBCЃН6ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКCP1ЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрAP1ЃН10Љ2![]() ЃЌМДP1ЃЈ6ЃЌ10Љ2
ЃЌМДP1ЃЈ6ЃЌ10Љ2![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБBP2ЃНDP2ЪБЃЌДЫЪБP2ЃЈ6ЃЌ6ЃЉЃЛ
ЂлЕБDBЃНDP3ЃН8ЪБЃЌ
дкRtЁїDEP3жаЃЌDEЃН6ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКP3EЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрAP3ЃНAE+EP3ЃН2![]() +2ЃЌМДP3ЃЈ6ЃЌ2
+2ЃЌМДP3ЃЈ6ЃЌ2![]() +2ЃЉЃЌ
+2ЃЉЃЌ
злЩЯЃЌТњзуЬтвтЕФPзјБъЮЊЃЈ6ЃЌ6ЃЉЛђЃЈ6ЃЌ2![]() +2ЃЉЛђЃЈ6ЃЌ10Љ2
+2ЃЉЛђЃЈ6ЃЌ10Љ2![]() ЃЉЃЎ
ЃЉЃЎ
ЕуОІЁПДЫЬтЪєгквЛДЮКЏЪ§злКЯЬтЃЌЩцМАЕФжЊЪЖгаЃКД§ЖЈЯЕЪ§ЗЈШЗЖЈвЛДЮКЏЪ§НтЮіЪНЃЌзјБъгыЭМаЮаджЪЃЌЕШбќШ§НЧаЮЕФЖЈвхЃЌЙДЙЩЖЈРэЃЌРћгУСЫЗжРрЬжТлЕФЫМЯыЃЌЪьСЗеЦЮеД§ЖЈЯЕЪ§ЗЈЪЧНтБОЬтЕквЛЮЪЕФЙиМќЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЦНааЫФБпаЮABCDЕФЖдНЧЯпACЕФДЙжБЦНЗжЯпгыБпADЁЂBCЗжБ№ЯрНЛгкЕуEЁЂFЃЎ
ЧѓжЄЃКЫФБпаЮAFCEЪЧСтаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЌЁїABC, ЁЯABCЁЂЁЯACB ЕФШ§ЕШЗжЯпНЛгкЕу EЁЂDЃЌ ШєЁЯ1=130ЁуЃЌЁЯ2=110ЁуЃЌЧѓЁЯA ЕФЖШЪ§ЁЃ
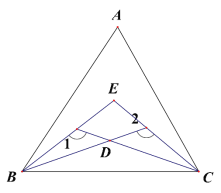
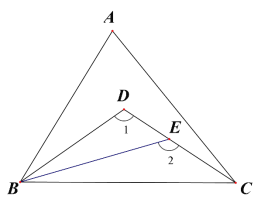
ЃЈ2ЃЉШчЭМЃЌЁїABC,ЁЯABC ЕФШ§ЕШЗжЯпЗжБ№гыЁЯACB ЕФЦНЗжЯпНЛгкЕу D,E ШєЁЯ1=110ЁуЃЌЁЯ2=130ЁуЃЌЧѓЁЯA ЕФЖШЪ§ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
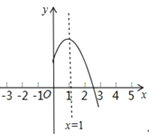
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌaЁй0ЃЉЭМЯѓЕФЖдГЦжсЪЧжБЯпx=1ЃЌЦфЭМЯѓЕФвЛВПЗжШчЭМЫљЪОЃЌЖдгкЯТСаЫЕЗЈЃКЂйabcЃМ0ЃЛЂкaЉb+cЃМ0ЃЛЂл3a+cЃМ0ЃЛЂмЕБЉ1ЃМxЃМ3ЪБЃЌyЃО0ЃЎЦфжае§ШЗЕФЪЧ______ЃЈАбе§ШЗЫЕЗЈЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЪЧA(1ЃЌ1)ЃЌB(4ЃЌ1)ЃЌC(3ЃЌ3)ЃЎ
(1)ЯШзїГіЁїABCЃЌдйНЋЁїABCЯђЯТЦНвЦ5ИіЕЅЮЛГЄЖШКѓЕУЕНЁїA1B1C1ЃЌЧыЛГіЁїA1B1C1ЃЛ
(2)НЋЁїABCШЦдЕуOФцЪБеыа§зЊ90ЁуКѓЕУЕУЕНЁїA2B2C2ЃЌЧыЛГіЁїA2B2C2ЃЛ
(3)ЧѓГівдOЃЌA1ЃЌBЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌзјБъдЕуOЪЧСтаЮABOCЕФвЛИіЖЅЕуЃЌБпOBТфдкxжсЕФИКАыжсЩЯЃЌЧвcosЁЯBOC=![]() ЃЌЖЅЕуCЕФзјБъЮЊ(aЃЌ4)ЃЌЗДБШР§КЏЪ§
ЃЌЖЅЕуCЕФзјБъЮЊ(aЃЌ4)ЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓгыСтаЮЖдНЧЯпAOНЛгкDЕуЃЌСЌНгBDЃЌЕБBDЁЭxжсЪБЃЌkЕФжЕЪЧЃЈЁЁЁЁЃЉ
ЕФЭМЯѓгыСтаЮЖдНЧЯпAOНЛгкDЕуЃЌСЌНгBDЃЌЕБBDЁЭxжсЪБЃЌkЕФжЕЪЧЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌDЪЧBCЕФжаЕуЃЌDEЁЭBCЃЌCE//ADЃЌШєACЃН2ЃЌCEЃН4ЃЌдђЫФБпаЮACEBЕФжмГЄЮЊ Ёј ЃЎ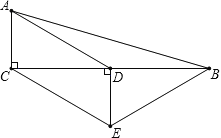
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
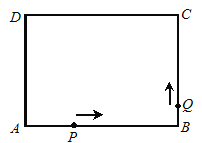
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН4ЃЌBCЃН3ЃЌЕуPЁЂQЗжБ№ДгAЁЂBСНЕуГіЗЂЃЌАДФцЪБеыЗНЯђбиОиаЮЕФБпдЫЖЏЃЌЕуPЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЌЕуQЕФЫйЖШЪЧУПУы1ИіЕЅЮЛГЄЖШЃЌдЫЖЏЕФЪБМфЮЊtУыЃЌЕБЦфжаФГвЛЕуЕНДяЕуAЪБЃЌдЫЖЏЭЃжЙЃЌдЫЖЏЙ§ГЬжаЃЌЕуPЙигкжБЯпAQЕФЖдГЦЕуМЧЮЊЕуMЃЎ
ЃЈ1ЃЉЕуPЕудкЯпЖЮABЩЯдЫЖЏЃЌЕуQдкЯпЖЮBCЩЯдЫЖЏЪБЃЌЧыгУКЌtЕФЪНзгБэЪОГіЁїAPQЕФУцЛ§SЃЛ
ЃЈ2ЃЉЕБЕуPдкЯпЖЮBCЩЯдЫЖЏЃЌЧвЁїABPЁзЁїPCQЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉШєЕуQдкЯпЖЮCDЩЯЃЌЧввдAЁЂPЁЂQЁЂMЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЃЌввСНМвЦћГЕЯњЪлЙЋЫОИљОнНќМИФъЕФЯњЪлСПЗжБ№жЦзїСЫШчЭМЫљЪОЕФЭГМЦЭМЃЌДг2014ЁЋ2018ФъЃЌетСНМвЙЋЫОжаЯњЪлСПдіГЄНЯПьЕФЪЧ_____ЙЋЫО(ЬюЁАМзЁБЛђЁАввЁБ)ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com