Question

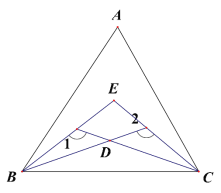
【题目】（1）如图，△ABC, ∠ABC、∠ACB 的三等分线交于点 E、D， 若∠1=130°，∠2=110°，求∠A 的度数。

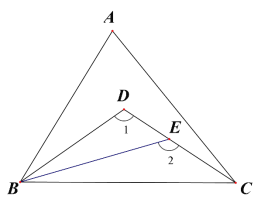
（2）如图，△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E 若∠1=110°，∠2=130°，求∠A 的度数。

Answer 1

【答案】（1）∠A=60°，（2）∠A=60°

【解析】

(1)由三角形内角和及三等角平分线的定义可得到方程组，则可求得∠ABC+∠ACB，再利用三角形内角和可求得∠A．

（2）由三角形外角可得∠DBC=20°由三等角平分线的定义可得∠ABC=60°，三角形内角和可得∠ECB=30°，角平分线的定义可得∠ACB=60°，由三角形内角和可得∠A=60°。

解：（1）

∵∠ABC、∠ACB 的三等分线交于点 E、D

, ∠ABC=3x，∠ACB=3y

①+②得：240°+3x+3y=360°

即3x+3y=120°

∴∠ABC+∠ACB=120°

∴∠A=180°-(∠ABC+∠ACB)=180°-120°=60°

（2）∵∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E