练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，平面直角坐标系中有一个四边形ABCD．

    （1）分别写出点A，B，C，D的坐标；

    （2）求四边形ABCD的面积；

    （3）将四边形ABCD先向下平移3个单位长度，再向右平移4个单位长度后得到的四边形A1B1C1D1，画出四边形A1B1C1D1

    【答案】见解析

    【解析】

    （1）根据平面直角坐标系中点与坐标的对应关系写出即可；

    （2）根据S四边形ABCD=S△ACB+S△ACD计算即可；

    （3）先画出四边形ABCD平移后的对应顶点A1、B1、C1、D1，然后用线段顺次连接即可.

    （1）A（﹣2，4），B（﹣4，0），C（﹣2，﹣1），D（0，1）；

    （2）S四边形ABCD=S△ACB+S△ACD=×5×4=10，

    （3）四边形A1B1C1D1如图所示．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，点E是AD的中点，延长BC到点F，使CF：BC=1：2，连接DF，EC．若AB=5，AD=8，sinB= ，则DF的长等于（ ）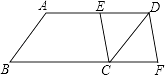
    A.
    B.
    C.
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD内接于半圆O，已知∠ADC=140°，则∠AOC的大小是（ ）
    A.40°
    B.60°
    C.70°
    D.80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知顶点为（﹣3，﹣6）的抛物线y=ax2+bx+c经过点（﹣1，﹣4），则下列结论中错误的是（ ）
    A.b2＞4ac
    B.ax2+bx+c≥﹣6
    C.若点（﹣2，m），（﹣5，n）在抛物线上，则m＞n
    D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】大学生小刘回乡创办小微企业，初期购得原材料若干吨，每天生产相同件数的某种产品，单件产品所耗费的原材料相同．当生产6天后剩余原材料36吨，当生产10天后剩余原材料30吨．若剩余原材料数量小于或等于3吨，则需补充原材料以保证正常生产．

    （1）求初期购得的原材料吨数与每天所耗费的原材料吨数；

    （2）若生产16天后，根据市场需求每天产量提高20%，则最多再生产多少天后必须补充原材料？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图，纸片□ABCD中，AD＝5，S□ABCD＝15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE'的位置，拼成四边形AEE'D，则四边形AEE'D的形状为( )

    A．平行四边形 B．菱形 C．矩形 D．正方形

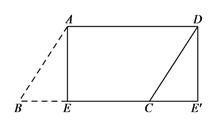
    (2)如图，在(1)中的四边形纸片AEE'D中，在EE'上取一点F，使EF＝4，剪下△AEF，剪下△AEF，将它平移至△DE'F'的位置，拼成四边形AFF'D．

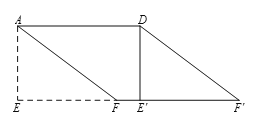
    ①求证：四边形AFF'D是菱形；

    ②求四边形AFF'D的两条对角线的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    点A、B、C为数轴上三点，如果点C在A、B之间且到A的距离是点C到B的距离3倍，那么我们就称点C是{ A，B }的奇点．

    例如，如图1，点A表示的数为﹣3，点B表示的数为1．表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{ A，B }的奇点；又如，表示﹣2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B }的奇点，但点D是{B，A}的奇点．

    （知识运用）

    如图2，M、N为数轴上两点，点M所表示的数为﹣3，点N所表示的数为5．

    （1）数　 　所表示的点是{ M，N}的奇点；数　 　所表示的点是{N，M}的奇点；

    （2）如图3，A、B为数轴上两点，点A所表示的数为﹣50，点B所表示的数为30．现有一动点P从点B出发向左运动，到达点A停止．P点运动到数轴上的什么位置时，P、A和B中恰有一个点为其余两点的奇点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD的边长为acm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是cm2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD的边长为acm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是cm2 ．

    查看答案和解析>>

    同步练习册答案