
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( ) 
A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
【答案】C
【解析】解:A、图象与x轴有两个交点,方程ax2+bx+c=0有两个不相等的实数根,b2﹣4ac>0所以b2>4ac,故A选项正确; B、抛物线的开口向上,函数有最小值,因为抛物线的最小值为﹣6,所以ax2+bx+c≥﹣6,故B选项正确;
C、抛物线的对称轴为直线x=﹣3,因为﹣5离对称轴的距离大于﹣2离对称轴的距离,所以m<n,故C选项错误;
D、根据抛物线的对称性可知,(﹣1,﹣4)关于对称轴的对称点为(﹣5,﹣4),所以关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1,故D选项正确.
故选C.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A. 商贩A的单价大于商贩B的单价
B. 商贩A的单价等于商贩B的单价
C. 商版A的单价小于商贩B的单价
D. 赔钱与商贩A、商贩B的单价无关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在一次数学考试中,从某班随机抽取的10名学生得分(单位:分)如下:75,85,90,90,95,85,95,95,100,98.
(1)求这10名学生得分的众数、中位数和平均数;
(2)若该班共有40名学生,估计此次考试的平均成绩约为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)在上学期的几次测试中,小张和小王的几次数学成绩(单位:分)如下表:

两人都说自己的数学成绩更好.请你想一想:
(1)小张可能是根据什么来判断的?小王可能是根据什么来判断的?
(2)你能根据小张的想法设计一种方案使小张的成绩比小王的高吗?写出你的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ![]() ,求AQ的长.
,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:课本上有这样一道例题:“解方程:![]()
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-![]() ④
④
请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中有一个四边形ABCD.
(1)分别写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积;
(3)将四边形ABCD先向下平移3个单位长度,再向右平移4个单位长度后得到的四边形A1B1C1D1,画出四边形A1B1C1D1

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( ) 
A.![]()
B.![]()
C.![]()
![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
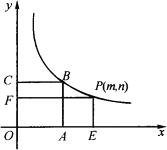
【题目】如图,正方形OABC的面积为9,点O为左边原点,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,点B在函数
轴上,点B在函数![]() 的图象上,点P
的图象上,点P![]() 是函数
是函数![]() 图象上的任意一点,过点P分别作
图象上的任意一点,过点P分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
(1)求B点坐标和![]() 值;
值;
(2)当![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com