
【题目】如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是 .

A. ① ② B. ① ② ③ C. ③ ④ D. ① ③
【答案】D
【解析】
根据抛物线与x轴的交点坐标为(1,0)对①进行判断;根据对称轴方程为![]() 对②进行判断;根据抛物线的对称性得到抛物线与x轴的交点坐标为(-3,0)和(1,0),由此对③进行判断;根据抛物线与y轴的交点在x轴下方,得到c<0,而a+b+c=0,则a-2b+c=-3b,由b>0,于是可对④进行判断.
对②进行判断;根据抛物线的对称性得到抛物线与x轴的交点坐标为(-3,0)和(1,0),由此对③进行判断;根据抛物线与y轴的交点在x轴下方,得到c<0,而a+b+c=0,则a-2b+c=-3b,由b>0,于是可对④进行判断.
∵x=1时,y=0,
∴a+b+c=0,所以①正确;
∵![]()
∴b=2a,所以②错误;
∵点(1,0)关于直线x=1对称的点的坐标为(3,0),
∴抛物线与x轴的交点坐标为(3,0)和(1,0),
∴ax2+bx+c=0的两根分别为3和1,所以③正确;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
而a+b+c=0,b=2a,
∴c=3a,
∴a2b+c=3b,
∵b>0,
∴3b<0,所以④错误.
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
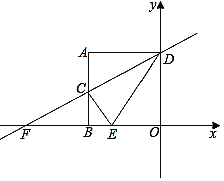
【题目】如图,A(-2,2)、AB⊥x轴于点B,AD⊥y轴于点D,C(-2,1)为AB的中点,直线CD交x轴于点F.
(1)求直线CD的函数关系式;
(2)过点C作CE⊥DF且交x轴于点E,求证:∠ADC=∠EDC;
(3)求点E坐标;
(4)点P是直线CE上的一个动点,求PB+PF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
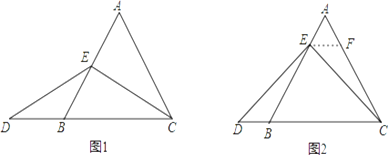
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俗话说“一铺养三代”。曾经,在市区繁华地段租一间门面,做点小生意,是不少人的生存之道。如今,这样的传统致富门道正在不断受到挑战。某服装店主,顺应时代潮流,在实体店销售的同时,开始网上销售。
(1)该店主某月线上线下共销售某款童装200件,其中网上销售量不低于实体销售量的4倍,求该店主该月实体销售量最多为多少?
(2)已知该店主5月实体销售该童装100件,每件获利18元;网上销售200件,每件获利12元。6月店主加大网上销售力度,网上销售每件获利较5月减少m%,但销售量比5月增加了2m%,实体店每件获利不变,销售量比5月减少了m%。结果该店主5月、6月线上线下获利总金额相同,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
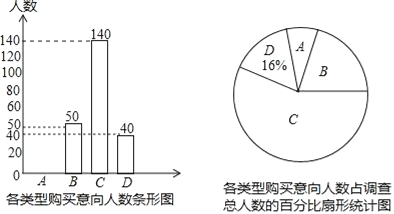
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
查看答案和解析>>
科目:初中数学 来源: 题型:
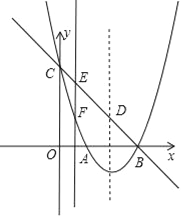
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子![]() 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=![]() 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=![]() (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com