
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
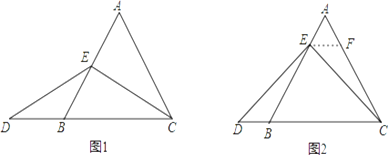
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
【答案】(1)=;(2)=;理由见解析;(3)3.
【解析】
(1)由E为等边三角形AB边的中点,利用三线合一得到CE垂直于AB,且CE为角平分线,由ED=EC,利用等边对等角及等腰三角形的性质得到一对角相等,利用等角对等边即可得证;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,由三角形ABC为等边三角形,得到三角形AEF为等边三角形,进而得到AE=EF=AF,BE=FC,再由ED=EC,以及等式的性质得到夹角相等,利用SAS得到三角形BDE与三角形EFC全等,利用全等三角形对应边相等得到DB=EF,等量代换即可得证;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,由BC+DB求出CD的长即可.
(1)当E为AB的中点时,AE=DB;
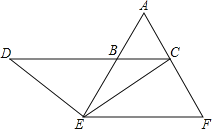
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,
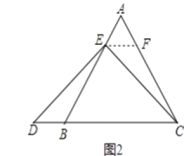
证明:∵△ABC为等边三角形,
∴△AEF为等边三角形,
∴AE=EF,BE=CF,
∵ED=EC,
∴∠D=∠ECD,
∵∠DEB=60°-∠D,∠ECF=60°-∠ECD,
∴∠DEB=∠ECF,
在△DBE和△EFC中,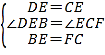 ,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
则AE=DB;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,
∴DB=EF=2,BC=1,
则CD=BC+DB=3.
故答案为:(1)=;(2)=(3)3


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线AB交y轴于A(0,a),交x轴于B(b,0),且a,b满足(a﹣b)2+|3a+5b﹣88|=0.
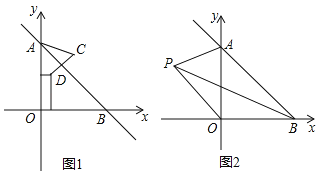
(1)求点A,B的坐标;
(2)如图1,已知点D(2,5),求点D关于直线AB对称的点C的坐标.
(3)如图2,若P是∠OBA的角平分线上的一点,∠APO=67.5°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两个直角三角形如图![]() 放置,使
放置,使![]() 与
与![]() 重合,
重合,![]() 与
与![]() 相交于点
相交于点![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 图
图![]() 中线段
中线段![]() 的长
的长![]() ________
________![]() ;
;![]() ________
________![]()
![]() 如图
如图![]() ,把
,把![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() 得
得![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() 恰好是以
恰好是以![]() 为底边的等腰三角形,求线段
为底边的等腰三角形,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,在边长为
,在边长为![]() 的小正方形组成的网格中,
的小正方形组成的网格中,![]() 的顶点
的顶点![]() 、
、![]() 均在格点上,点
均在格点上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .
.

![]() 点
点![]() 关于点
关于点![]() 中心对称的点的坐标为________;
中心对称的点的坐标为________;
![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到
后得到![]() ,那么点
,那么点![]() 的坐标为________;线段
的坐标为________;线段![]() 在旋转过程中所扫过的面积是________.
在旋转过程中所扫过的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=20 cm,P,Q,M,N分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2 cm,
(1)当x为何值时,点P,N重合;
(2)当x为何值是,以P,Q,M,N为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,羊年春节到了,小明亲手制作了![]() 张一样的卡片,在每张卡片上分别写上“新”“年”“好”三个字,并随机放入一个不透明的信封中,然后让小芳分三次从信封中摸
张一样的卡片,在每张卡片上分别写上“新”“年”“好”三个字,并随机放入一个不透明的信封中,然后让小芳分三次从信封中摸![]() 张卡片(每次摸
张卡片(每次摸![]() 张,摸出不放回).
张,摸出不放回).
![]()
![]() 小芳第一次抽取的卡片是“新”字的概率是多少?
小芳第一次抽取的卡片是“新”字的概率是多少?
![]() 请通过画树状图或列表,求小芳先后抽取的
请通过画树状图或列表,求小芳先后抽取的![]() 张卡片分别是“新年好”的概率.
张卡片分别是“新年好”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是 .

A. ① ② B. ① ② ③ C. ③ ④ D. ① ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com