
【题目】在平面直角坐标系中,直线AB交y轴于A(0,a),交x轴于B(b,0),且a,b满足(a﹣b)2+|3a+5b﹣88|=0.
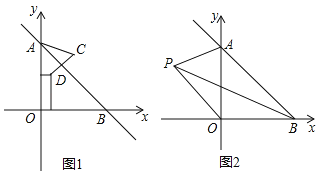
(1)求点A,B的坐标;
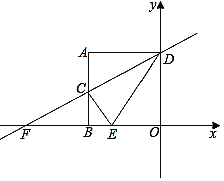
(2)如图1,已知点D(2,5),求点D关于直线AB对称的点C的坐标.
(3)如图2,若P是∠OBA的角平分线上的一点,∠APO=67.5°,求![]() 的值.
的值.
【答案】(1)A(0,11),B(11,0);(2)C的坐标为(6,9);(3)3
【解析】
(1)利用非负数的性质求出A、B两点坐标,再利用待定系数法切线直线AB解析式即可解决问题.
(2)延长FD交AB于点E,连结CE,易得△DEC,△AFE都是等腰直角三角形,再根据D(2,5),得到DG=5,进而得到AF=EF=6,最后得出C(6,9);
(3)利用角平分线的性质构造全等三角形,然后通过角度的关系得出边的关系即可.
解:(1)由题意得![]() ,
,
解得![]() ,
,
∴A(0,11),B(11,0);
(2)如图,延长FD交AB于点E,连结CE
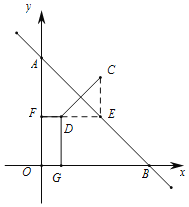
因为OB=OA=11,
所以三角形OAB是等腰直角三角形,
易得△DEC,△AFE都是等腰直角三角形,
所以FE=AF=OA﹣OF=11﹣5=6,
∴CE=DE=EF﹣FD=6﹣2=4,
所以C的横坐标为6.,纵坐标为5+4=9,
故C的坐标为(6,9);
(3)如图,作PM垂直AB于点M,作PM垂直OB于点L,在L的左侧取一点N,使得NL=AM,
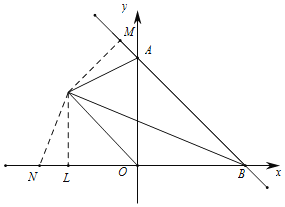
∵PB是∠ABO的平分线,
所以PM=PL,
∴△AMP≌△NLP,
∴∠NLP=∠APM,
∴∠APN=∠MPL.
∵∠ABO=45°,
∴∠MPL=135°,
∴∠APN=135°,
又∠APO=67.5°,
∴∠NPO=∠APO=67.5°.
∵PN=PA,PO=PO,
∴△OPN≌OPA,
∴∠PON=∠POA=45°,NO=AO=11,
设NL=a,则MA=a,
∴BL=BM=a+11![]() ,
,
∵BL=22﹣a,
∴22﹣a=a+11![]() ,
,
∴a=11﹣![]() ,
,
∴LO=11﹣(11﹣![]() )=
)=![]() ,
,
∴PO=![]() LO=11,
LO=11,
所以![]() =3.
=3.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动时,形状保持不变,且与
上运动时,形状保持不变,且与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),给出下列结论:①
的左侧),给出下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 随
随![]() 的增大而增大;③若点
的增大而增大;③若点![]() 的横坐标最大值为
的横坐标最大值为![]() ,则点
,则点![]() 的横坐标最小值为
的横坐标最小值为![]() ;④当四边形
;④当四边形![]() 为平行四边形时,
为平行四边形时,![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,
,![]() 是抛物线的顶点.
是抛物线的顶点.
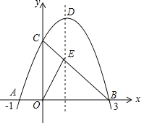
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 直接写出点
直接写出点![]() 和点
和点![]() 的坐标;
的坐标;
![]() 若点
若点![]() 在第一象限内的抛物线上,且
在第一象限内的抛物线上,且![]() ,求
,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若
,下列说法:①若![]() ,则方程必有一根为
,则方程必有一根为![]() ;②若
;②若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;③若
成立;③若![]() ,则方程
,则方程![]() 一定有两个不相等实数根;其中正确结论有( )个.
一定有两个不相等实数根;其中正确结论有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-2,2)、AB⊥x轴于点B,AD⊥y轴于点D,C(-2,1)为AB的中点,直线CD交x轴于点F.
(1)求直线CD的函数关系式;
(2)过点C作CE⊥DF且交x轴于点E,求证:∠ADC=∠EDC;
(3)求点E坐标;
(4)点P是直线CE上的一个动点,求PB+PF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
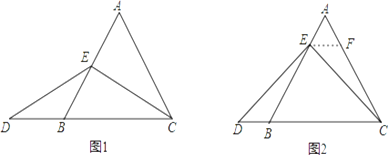
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com