
【题目】如图,点O是直线AB上一点,∠BOC=120°,OD平分∠AOC.
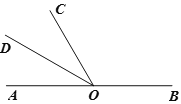
(1)求∠COD的度数.
请你补全下列解题过程.
∵点O为直线AB上一点,
∴∠AOB=_____.
∵∠BOC =120°,
∴∠AOC=______.
∵OD 平分∠AOC,
∴∠COD=![]() ∠AOC.( )
∠AOC.( )
∴∠COD=________.
(2)若E是直线AB外一点,满足∠COE:∠BOE=4:1直接写出∠BOE的度数.
【答案】(1)180°;60°;角平分线定义;30°;(2)24°或40°.
【解析】
(1)利用∠BOC=120°及补角的性质就可求出∠AOC的度数,根据角平分线的定义就可求出∠COD的度数;
(2)分OE在∠BOC内部和OE在∠BOC外部两种情况进行计算.
解:(1)∵点O为直线AB上一点,
∴∠AOB= 180° .
∵∠BOC =120°,
∴∠AOC= 60° .
∵OD 平分∠AOC,
∴∠COD=![]() ∠AOC.(角平分线定义)
∠AOC.(角平分线定义)
∴∠COD= 30° ;
(2)如图,当OE在∠BOC内部时,
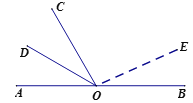
∵∠BOC=120°,∠COE:∠BOE=4:1,
∴∠BOE=![]() ∠BOC=24°;
∠BOC=24°;
如图,当OE在∠BOC外部时,
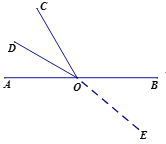
∵∠BOC=120°,∠COE:∠BOE=4:1,
∴![]() =
=![]() ,
,
∴∠BOE=40°.
故答案为:(1)180°;60°;角平分线定义;30°;(2)24°或40°.


科目:初中数学 来源: 题型:
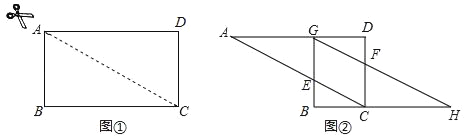
【题目】如图①,将一个长方形沿着对角线剪开即可得到两个全等的三角形,再把△ABC沿着AC方向平移,得到图②中的△GBH,BG交AC于点E,GH交CD于点F.在图②中,除△ACD与△HGB全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
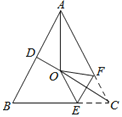
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的点P,Q,给出如下定义:若点P到点Q的距离为d(d≥0),则称d为点P到点Q的d追随值,记作d[PQ].例如,在数轴上点P表示的数是2,点Q表示的数是5,则点P到点Q的d追随值为d[PQ]=3.
问题解决:
(1)点M,N都在数轴上,点M表示的数是1,且点N到点M的d追随值d[MN]=a(a≥0),则点N表示的数是_____(用含a的代数式表示);
(2)如图,点C表示的数是1,在数轴上有两个动点A,B都沿着正方向同时移动,其中A点的速度为每秒3个单位,B点的速度为每秒1个单位,点A从点C出发,点B表示的数是b,设运动时间为t(t>0).
①当b=4时,问t为何值时,点A到点B的d追随值d[AB]=2;
②若0<t≤3时,点A到点B的d追随值d[AB]≤6,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:

(1)FC=AD;
(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
-3,0.2,0,-|+![]() |,-5%,-
|,-5%,-![]() ,|-9|,-(-1),-23,+3
,|-9|,-(-1),-23,+3![]() .
.
(1)正整数集合:{ …};
(2)负分数集合:{ …};
(3)负数集合:{ …};
(4)整数集合:{ …};
(5)分数集合:{ …};
(6)非负数集合:{ …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com