
【题目】如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,∠BOC=120°,OD平分∠AOC.
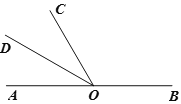
(1)求∠COD的度数.
请你补全下列解题过程.
∵点O为直线AB上一点,
∴∠AOB=_____.
∵∠BOC =120°,
∴∠AOC=______.
∵OD 平分∠AOC,
∴∠COD=![]() ∠AOC.( )
∠AOC.( )
∴∠COD=________.
(2)若E是直线AB外一点,满足∠COE:∠BOE=4:1直接写出∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值 x(x﹣1)+2x(x+1)﹣(3x﹣1)(2x﹣5),其中 x=2.
(2)解方程(3x﹣2)(2x﹣3)=(6x+5)(x﹣1)+15.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( ) 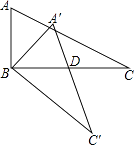
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;其中正确的有( )
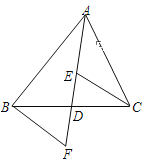
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A在数轴上对应的数为![]() 点B对应的数为
点B对应的数为![]() 且
且![]() 满足
满足![]()
(1)线段AB的长为________;
(2)点C在数轴上对应的数为10,在数轴上是否存在点D,使得DA+DB=DC?若存在,求出点D对应的数;若不存在,说明理由。
(3)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左均速运动;动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左移动;动点M从点A出发,以每秒3个单位长度的速度沿数轴向左均速移动,点P、Q、M同时出发,设运动时间为![]() 秒,当
秒,当![]() 时,探究QP、QA、QM三条线段之间的数量关系,并说明理由.
时,探究QP、QA、QM三条线段之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com