
【题目】如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( ) 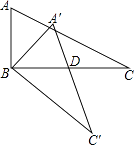
A.![]()
B.![]()
C.![]()
D.2 ![]()
【答案】B
【解析】解:过点B作BM⊥A′C′,交A′C′于点M,如图所示: 
∵∠ABC=90°,AB=2,BC=4,
∴AC= ![]() =
= ![]() =2
=2 ![]() ,cosA=
,cosA= ![]() =
= ![]() =
= ![]() ,
,
由题意得:∠A′=∠A,A′B=AB=2,A′C′=AC=2 ![]() ,
,
∵点D为BC的中点,
∴BD= ![]() BC=2,BD=A′B,而BM⊥A′C′,
BC=2,BD=A′B,而BM⊥A′C′,
∴A′M=DM,
∵cosA′=cosA,且cosA′= ![]() ,
,
∴A′M= ![]() ×2=
×2= ![]() ,
,
∴C'D=A'C'﹣2A'M=2 ![]() ﹣2×
﹣2× ![]() =
= ![]() ,
,
所以答案是:B.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对于数轴上的点P,Q,给出如下定义:若点P到点Q的距离为d(d≥0),则称d为点P到点Q的d追随值,记作d[PQ].例如,在数轴上点P表示的数是2,点Q表示的数是5,则点P到点Q的d追随值为d[PQ]=3.
问题解决:
(1)点M,N都在数轴上,点M表示的数是1,且点N到点M的d追随值d[MN]=a(a≥0),则点N表示的数是_____(用含a的代数式表示);
(2)如图,点C表示的数是1,在数轴上有两个动点A,B都沿着正方向同时移动,其中A点的速度为每秒3个单位,B点的速度为每秒1个单位,点A从点C出发,点B表示的数是b,设运动时间为t(t>0).
①当b=4时,问t为何值时,点A到点B的d追随值d[AB]=2;
②若0<t≤3时,点A到点B的d追随值d[AB]≤6,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏在测量学校一幢教学楼AB的高度时,她先在点C测得教学楼的顶部A的仰角为30°,然后向教学楼前进12米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.
(结果精确到0.1米,参考数据: ![]() ≈1.73)
≈1.73)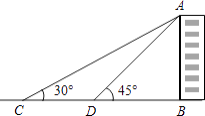
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
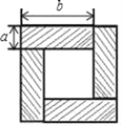
【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们都知道,![]()
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为![]() ,所以
,所以![]() ,
,![]()
所以,-2x2+40x+5有最大值205.
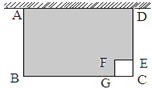
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF 
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com