
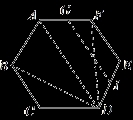
边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )

A. B.
B. C.
C. D.
D.
A
【解析】
连接AD、DB、DF,求出∠AFD=∠ABD=90°,根据HL证两三角形全等得出∠FAD=60°,求出AD∥EF∥GI,过F作FZ⊥GI,过E作EN⊥GI于N,得出平行四边形FZNE得出EF=ZN=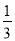 a,求出GI的长,求出第一个正六边形的边长是
a,求出GI的长,求出第一个正六边形的边长是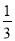 a,是等边三角形QKM的边长的
a,是等边三角形QKM的边长的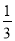 ;同理第二个正六边形的边长是等边三角形GHI的边长的
;同理第二个正六边形的边长是等边三角形GHI的边长的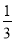 ;求出第五个等边三角形的边长,乘以
;求出第五个等边三角形的边长,乘以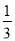 即可得出第六个正六边形的边长.
即可得出第六个正六边形的边长.
连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中
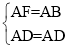
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=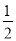 ×120°=60°,
×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
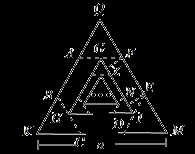
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是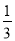 a,即等边三角形QKM的边长的
a,即等边三角形QKM的边长的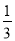 ,
,
过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=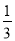 a,
a,
∵GF=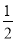 AF=
AF=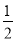 ×
×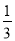 a=
a=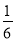 a,∠FGI=60°(已证),
a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=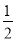 GF=
GF=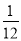 a,
a,
同理IN=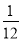 a,
a,
∴GI=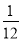 a+
a+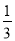 a+
a+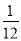 a=
a=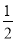 a,即第二个等边三角形的边长是
a,即第二个等边三角形的边长是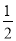 a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是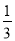 ×
×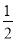 a;
a;
同理第第三个等边三角形的边长是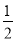 ×
×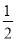 a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是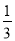 ×
×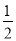 ×
×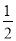 a;
a;
同理第四个等边三角形的边长是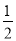 ×
×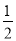 ×
×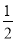 a,第四个正六边形的边长是
a,第四个正六边形的边长是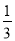 ×
×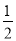 ×
×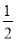 ×
×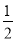 a;
a;
第五个等边三角形的边长是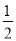 ×
×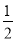 ×
×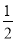 ×
×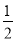 a,第五个正六边形的边长是
a,第五个正六边形的边长是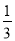 ×
×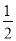 ×
×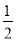 ×
×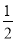 ×
×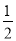 a;
a;
第六个等边三角形的边长是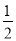 ×
×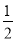 ×
×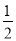 ×
×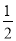 ×
×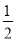 a,第六个正六边形的边长是
a,第六个正六边形的边长是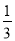 ×
×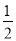 ×
×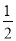 ×
×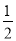 ×
×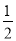 ×
×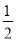 a,
a,
即第六个正六边形的边长是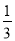 ×
×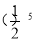 a,
a,
故选A.


科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.1练习卷(解析版) 题型:选择题
在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.1练习卷(解析版) 题型:填空题
如图,已知AB∥CD,∠A=α,∠C=β,∠ABC和∠CDA的平分线交于E1,∠E1BC和∠E1DA的平分线交于E2,∠E2BC和∠E2DA的平分线交于E3,按如此方式继续下去…,用α,β的代数式表示∠BEnD的度数为 .
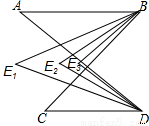
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等腰三角形练习卷(解析版) 题型:选择题
等腰三角形的一条边长为6,另一边长为13,则它的周长为( )
A.25 B.25或32 C.32 D.19
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等边三角形练习卷(解析版) 题型:选择题
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
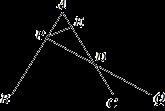
A. B.
B. C.
C. D.不能确定
D.不能确定
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等腰三角形练习卷(解析版) 题型:填空题
如图,在△ABC中,∠ABC=∠C=2∠A,BD⊥AC交AC于点D,则∠DBC= .

查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等腰三角形练习卷(解析版) 题型:填空题
如图.点D、E在△ABC的边BC上,AB=AC,AD=AE.请写出图中的全等三角形 (写出一对即可).

查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等腰三角形练习卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述结论一定正确的是( )

A.①②③ B.②③④ C.①③⑤ D.①③④
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等边三角形练习卷(解析版) 题型:填空题
如图所示,边长为2的等边三角形木块,沿水平线l滚动,则A点从开始至结束所走过的路线长为: (结果保留准确值).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com