
【题目】在平面直角坐标系![]() 中,如图所示,已知
中,如图所示,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,在
轴上,在![]() 中,点
中,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() .
.![]() ,
,![]() ,
,![]() .按下列要求画图(保留作图痕迹):
.按下列要求画图(保留作图痕迹):
(1)将![]() 绕
绕![]() 点按逆时针方向旋转90°得到
点按逆时针方向旋转90°得到![]() (其中点
(其中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ),画出
),画出![]() .
.
(2)将![]() 沿
沿![]() 轴向右平移得到
轴向右平移得到![]() (其中点
(其中点![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ),使得边
),使得边![]() 与(1)中的
与(1)中的![]() 的边
的边![]() 重合.
重合.
(3)求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)6
【解析】
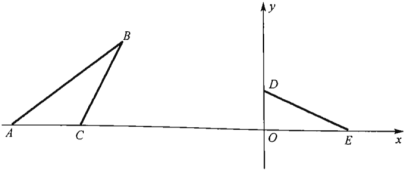
(1)以点O为圆心,以OE为半径画弧,与y轴正半轴相交于点N,以OD为半径画弧,与x轴负半轴相交于点M,连接MN即可;
(2)以M为圆心,以AC长为半径画弧与x轴负半轴相交于点A',B'与N重合,C'与M重合,然后顺次连接即可;
(3)设OE=x,则ON=x,作MF⊥A'B'于点F,判断出B'C'平分∠A'B'O,再根据全等三角形的性质可得B'F=B'O=OE=x,FC'=OC'=OD=3,利用勾股定理列式求出A'F,然后表示出A'B'、A'O.在Rt△A'B'O中,利用勾股定理列出方程求解即可.
(1)△OMN如图所示;
(2)△A'B'C'如图所示;
(3)设OE=x,则ON=x,作MF⊥A'B'于点F,
由作图可知:B'C'平分∠A'B'O,且C'O⊥OB',
∴∠B'FM=∠MON=90°,∠FB'M=∠OB'M.
∵B'M=B'M,
∴△FB'M≌△OB'M,
∴B'F=B'O=OE=x,FC'=OC'=OD=3.
∵A'C'=AC=5,
∴A'F![]() 4,
4,
∴A'B'=x+4,A'O=5+3=8,
在Rt△A'B'O中,x2+82=(4+x)2,
解得:x=6,
即OE=6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】学校冬季趣味运动会开设了“抢收抢种”项目,八(5)班甲、乙两个小组都想代表班级参赛,为了选择一个比较好的队伍,八(5)班的班委组织了一次选拔赛,甲、乙两组各10人的比赛成绩如下表:
甲组 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙组 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲组成绩的中位数是 分,乙组成绩的众数是 分.
(2)计算乙组的平均成绩和方差.
(3)已知甲组成绩的方差是1.4,则选择 组代表八(5)班参加学校比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
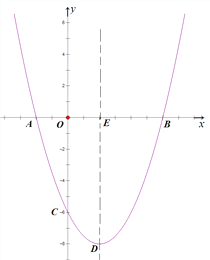
【题目】(题文)如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强在做课后习题时,遇到这样一道题:“如图所示,![]() 、
、![]() 两村庄在一条河的两岸,从
两村庄在一条河的两岸,从![]() 村庄去
村庄去![]() 村庄,需要在河上造一座桥
村庄,需要在河上造一座桥![]() ,请问桥造在何处从
,请问桥造在何处从![]() 村庄去
村庄去![]() 村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
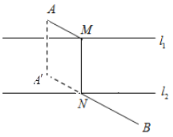
小强的解题思路,因为桥与河岸垂直,线段![]() 是一个不变的量,将它平移到
是一个不变的量,将它平移到![]() 处得线段
处得线段![]() ,总的路程
,总的路程![]() 与
与![]() 是相等的,故要使
是相等的,故要使![]() 最短,就是求点
最短,就是求点![]() 到点
到点![]() 最短即可,所以点
最短即可,所以点![]() 应是
应是![]() 与
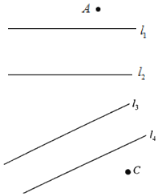
与![]() 的交点.根据上述材料解答下列问题:如图所示:
的交点.根据上述材料解答下列问题:如图所示:![]() 、
、![]() 两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从
两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从![]() 地出发到
地出发到![]() 地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河
地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河![]() 与
与![]() 的宽为
的宽为![]() ,河
,河![]() 与
与![]() 的宽为
的宽为![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m-1)x-2m2+m=0(m为实数)有两个实数根x1、x2.
(1)当m为何值时,x1=x2.
(2)若x12+x22,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
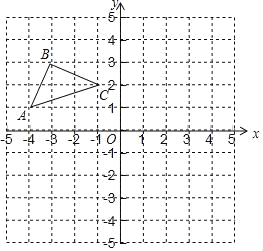
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标:A1( ),B1( ),C1( );
(2)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2,连接C1C2,CC2,C1C,并直接写出△CC1C2的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com