
分析 首先根据题意画出几何图形,再设AD=2,则BC=5,FD=1,EC=3,GF:GE=FD:EC=1:3,GF:FE=1:2,S△GFD:S△FED=GF:FE=1:2,S△EFD:S△CED=FD:EC=1:3即可得出答案.
解答 解:如图所示:
设AD=2,则BC=5,FD=1,EC=3,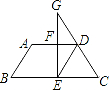
∵GF:GE=FD:EC=1:3,GF:FE=1:2,S△GFD:S△FED=GF:FE=1:2,
显然有S△EFD:S△CED=FD:EC=1:3,
∴S△GFD:S△FED:S△CED=1:2:6.
故答案为:1:2:6.
点评 本题考查了相似三角形的性质以及梯形的有关知识,属于基础题,正确运用边的比例关系求解是解题关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菱形ABCD的对角线AC、BD的长分别为4和2,若直线l满足:①点A到直线l的距离为$\sqrt{3}$;②B、D两点到直线l的距离相等.则符合题意的直线l的条数为( )
菱形ABCD的对角线AC、BD的长分别为4和2,若直线l满足:①点A到直线l的距离为$\sqrt{3}$;②B、D两点到直线l的距离相等.则符合题意的直线l的条数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间,射线最短 | B. | 两点确定一条直线 | ||
| C. | 两点之间,直线最短 | D. | 两点之间,线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com