
【题目】如图,直线![]() ,点
,点![]() 在直线
在直线![]() 上,以点
上,以点![]() 为圆心,适当长度为半径画弧,分别交直线
为圆心,适当长度为半径画弧,分别交直线![]() ,
,![]() 于
于![]() ,
,![]() 两点,以点
两点,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与前弧交于点
长为半径画弧,与前弧交于点![]() (不与点
(不与点![]() 重合),连接
重合),连接![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 交
交![]() 于点
于点![]() .若
.若![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
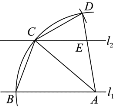
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
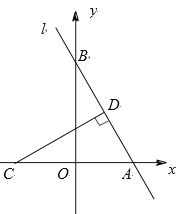
(1)求点D,O之间的距离;
(2)当tan∠CDO=![]() 时,求直线l的解析式;
时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上存在点P、点M与线段AB.若线段AB上存在一点Q,使得点M在以PQ为直径的圆上,则称点M为点P与线段AB的共圆点.
已知点P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
(1)在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是 ;
(2)点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;
(3)已知点M(m,﹣1),若直线y=![]() x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
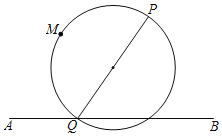
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(不与点A,B重合),AB=6cm,过点C作CD⊥AB于点D,E是CD的中点,连接AE并延长交![]() 于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.
于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.

下面是小腾的探究过程,请补充完整:
(1)对于点C在![]() 上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |
在AC,CD,FD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;

(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质并解决问题.
的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)取几组![]() 与
与![]() 的对应值,填写在下表中.
的对应值,填写在下表中.
| … |
|
|
| 0 | 1 | 1.2 | 1.25 | 2.75 | 2.8 | 3 | 4 | 5 | 6 | 8 | … |
| … | 1 | td style="width:6%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">2 | 3 | 6 | 7.5 | 8 | 8 | 7.5 | 6 | 3 |
| 1.5 | 1 | … |
![]() 的值为_____________;
的值为_____________;
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
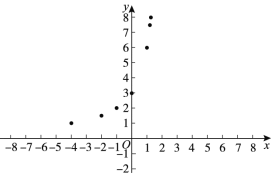
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数![]() 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;
②过点![]() 作直线
作直线![]() 轴,与函数
轴,与函数![]() 的图象交于点
的图象交于点![]() (点
(点![]() 在点
在点![]() 的左侧),则
的左侧),则![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
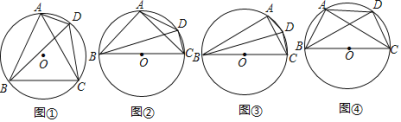
【题目】(1)方法选择
如图①,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
小颖认为可用截长法证明:在![]() 上截取
上截取![]() ,连接
,连接![]() …
…
小军认为可用补短法证明:延长![]() 至点
至点![]() ,使得
,使得![]() …
…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() .试用等式表示线段
.试用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
(3)拓展猜想
如图④,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[提出问题]正多边形内任意一点到各边距离之和与这个正多边形的边及内角有什么关系?
[探索发现]
![]() 为了解决这个问题,我们不妨从最简单的正多边形-------正三角形入手
为了解决这个问题,我们不妨从最简单的正多边形-------正三角形入手
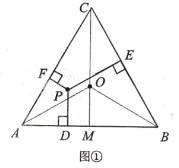
如图①,![]() 是正三角形,边长是
是正三角形,边长是![]() 是
是![]() 内任意一点,
内任意一点,![]() 到
到![]() 各边距离分别为
各边距离分别为![]() ,确定
,确定![]() 的值与
的值与![]() 的边及内角的关系.
的边及内角的关系.
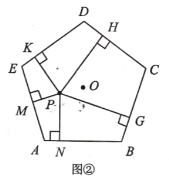
![]() 如图②,五边形
如图②,五边形![]() 是正五边形,边长是
是正五边形,边长是![]() 是正五边形
是正五边形![]() 内任意一点,
内任意一点,![]() 到五边形
到五边形![]() 各边距离分别为
各边距离分别为![]() , 参照
, 参照![]() 的探索过程,确定
的探索过程,确定![]() 的值与正五边形
的值与正五边形![]() 的边及内角的关系.
的边及内角的关系.
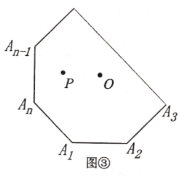
![]() 类比上述探索过程:
类比上述探索过程:
正六边形(边长为![]() )内任意一点
)内任意一点 ![]() 到各边距离之和
到各边距离之和![]()
正八边形(边长为![]() )内任意一点
)内任意一点![]() 到各边距离之和
到各边距离之和![]()
[问题解决]正![]() 边形(边长为
边形(边长为![]() )内任意-一点P到各边距离之和
)内任意-一点P到各边距离之和![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com