
分析 (1)原式利用题中的新定义计算即可得到结果;
(2)原式利用题中的新定义计算即可得到结果;
(3)已知等式利用题中的新定义化简,移项合并,把y系数化为1,即可求出解.
解答 解:(1)根据题中的新定义得:8△(-3)=(8-2)×3-2×(-3)=18+6=24;
(2)根据题中的新定义得:(-$\frac{1}{3}$)△(-5)=(-$\frac{1}{3}$-2)×3-2×(-5)=-1-6+10=3;
(3)根据题中的新定义化简得:(2y-2)×3-2(y-5)=(3-y-2)×3-2(-3y),
去括号得:6y-6-2y+10=3-3y+6y,
移项合并得:y=-1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{2}{7}$<a<$\frac{2}{5}$ | B. | -$\frac{2}{11}$<a<0 | C. | -$\frac{2}{7}$<a<0 | D. | a>-$\frac{2}{11}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读解答过程,回答问题:
阅读解答过程,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
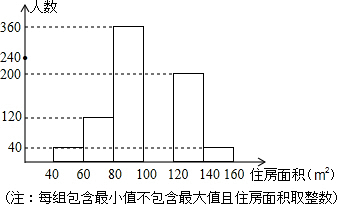 2008年我市春季住博会期间,某公司对参加本次房交会的消费者进行了问卷调查,制成表格如下:
2008年我市春季住博会期间,某公司对参加本次房交会的消费者进行了问卷调查,制成表格如下:| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 200 | 500 | 200 | 70 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com