
| A. | -$\frac{2}{7}$<a<$\frac{2}{5}$ | B. | -$\frac{2}{11}$<a<0 | C. | -$\frac{2}{7}$<a<0 | D. | a>-$\frac{2}{11}$ |
分析 根据根的判别式求出a的取值范围,再根据根与系数的关系求出a的取值范围,求其公共解即可.
解答 解:∵关于x的方程ax2+(a+2)x+9a=0有两个不相等的实数根x1、x2,
∴△=(a+2)2-4a•9a=a2+4a+4-36a2=-35a2+4a+4>0;
整理得(-5a+2)(7a+2)>0,
即$\left\{\begin{array}{l}{-5a+2>0}\\{7a+2>0}\end{array}\right.$,解得-$\frac{2}{7}$<a<$\frac{2}{5}$;
或$\left\{\begin{array}{l}{-5a+2<0}\\{7a+2<0}\end{array}\right.$,无解;
又∵x1<1<x2,
∴x1-1<0,x2-1>0,
∴(x1-1)(x2-1)<0,
即x1x2-(x1+x2)+1<0,
∵${x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{a+2}{a}$,${x}_{1}•{x}_{2}=\frac{c}{a}=\frac{9a}{a}=9$
根据根与系数的关系得,9-(-$\frac{a+2}{a}$)+1<0,
解得0>a>-$\frac{2}{11}$,
综上,-$\frac{2}{11}$<a<0.
故选:B.
点评 此题考查了抛物线与x轴的交点、一元二次方程的根与系数的关系,将这二者结合是解决此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ±10xy | B. | ±5xy | C. | 20xy | D. | $\frac{5}{2}$xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,C为线段AB上一点,D是线段AC的中点,E为线段CB的中点.
如图,C为线段AB上一点,D是线段AC的中点,E为线段CB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
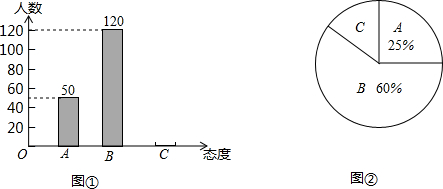
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com