
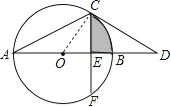
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1) 30°;(2)![]() -2
-2![]() .
.
【解析】试题分析:(1)连接OC,则△OCD是直角三角形,可求出∠COD的度数;由于∠A与∠COD是同弧所对的圆周角与圆心角.根据圆周角定理即可求得∠A的度数;
(2)由图可知:阴影部分的面积是扇形OCB和Rt△OEC的面积差;那么解决问题的关键是求出半径和OE的长;在Rt△OCE中,∠OCE=∠D=30°,已知了CE的长,通过解直角三角形,即可求出OC、OE的长,由此得解.
试题解析:(1)连接OC,
∵CD切⊙O于点C
∴∠OCD=90°
∵∠D=30°
∴∠COD=60°
∵OA=OC
∴∠A=∠ACO=30°;
(2)∵CF⊥直径AB,CF=4![]()
∴CE=2![]()
∴在Rt△OCE中,tan∠COE=![]() ,
,
OE=![]() =2,
=2,
∴OC=2OE=4
∴S扇形BOC=![]() ,S△EOC=
,S△EOC=![]() ×2×2
×2×2![]() =2
=2![]()
∴S阴影=S扇形BOC-S△EOC=![]() -2
-2![]() .
.


科目:初中数学 来源: 题型:
【题目】下列调查中适合采用抽样调查的是( )
A.调查本班同学的身高情况B.飞机起飞前,对相关零部件进行检查
C.调查春节联欢晚会的收视率D.选出某班短跑跑得最快的学生参加学校比赛
查看答案和解析>>
科目:初中数学 来源: 题型:
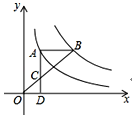
【题目】如图,点A在双曲线y=![]() 上,点B在双曲线y=
上,点B在双曲线y=![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
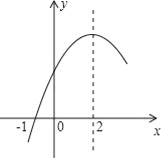
其中正确结论的序号是_______________.(在横线上填上你认为所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
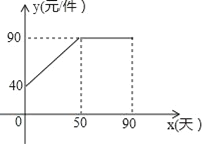
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某病毒细胞的直径约为0.000156cm,用科学记数法表示这个数是( )
A.0.156×10﹣3B.15.6×10﹣5C.1.56×10﹣4D.1.56×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.连接直线外一点与直线上各点的所有线段中,垂线段最短
B.互补的角是邻补角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com