
分析 由题意抛物线y=x2+bx+c与y轴交于点C,令x=0,求出C点坐标,又与x轴的负半轴交于A、B两点,判断出c的符号,将其转化为方程的两个根,再根据S△ABC=2,求出b值
解答 解:∵抛物线y=x2+bx+c与y轴交于点C,
令x=0得,C(0,c),
∵该抛物线的开口向上,且与x轴的负半轴交于A、B两点,
∴抛物线与y轴的交点在y轴的正半轴,
∴c>0,
设方程x2+bx+c=0的两个根为x1,x2,
∴x1+x2=-b,x1x2=c,
∵BC=2=|x1-x2|.
∵S△ABC=,
∴$\frac{1}{2}$BC×c=2,
∴c=2,
∵|x1-x2|=$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\sqrt{({x}_{1+}{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,
∴4=b2-8,
∴b=±2$\sqrt{3}$,
∵x1+x2=-b<0
∴b>0,
∴b=2$\sqrt{3}$.
点评 此题主要考查一元二次方程与函数的关系及三角形的面积公式,函数与x轴的交点的横坐标就是方程的根,两者可以互相转化.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
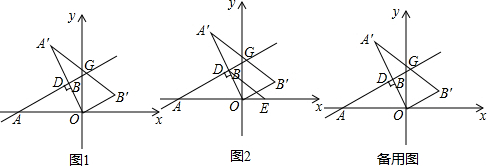
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
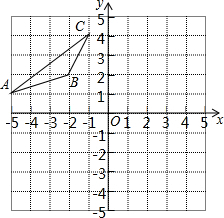 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com