
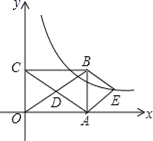
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
【答案】(1)见解析;(2)y=![]() .
.
【解析】试题分析:(1)先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,即可证出四边形AEBD是菱形;
(2)连接DE,交AB于F,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;设经过点E的反比例函数解析式为:y=![]() ,把点E坐标代入求出k的值即可.
,把点E坐标代入求出k的值即可.
(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=![]() AC,DB=
AC,DB=![]() OB,AC=OB,AB=OC=2,
OB,AC=OB,AB=OC=2,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=![]() OA=
OA=![]() ,AF=
,AF=![]() AB=1,3+
AB=1,3+![]() =
=![]() ,
,
∴点E坐标为:(![]() ,1),
,1),
设经过点E的反比例函数解析式为:y=![]() ,
,
把点E(![]() ,1)代入得:k=
,1)代入得:k=![]() ,
,
∴经过点E的反比例函数解析式为:y=![]() .
.



 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.

(1)若CD=CA=AB,请求出y与x的等量关系式;
(2)当D为边BC上一点,并且CD=CA,x=40,y=30时,则AB AC(填“=”或“≠”);
(3)如果把(2)中的条件“CD=CA”变为“CD=AB”,且x,y的取值不变,那么(1)中的结论是否仍成立?若成立请写出证明过程,若不成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
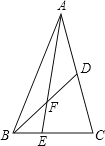
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运用平方差公式计算,错误的是( )
A. (a+b)(a﹣b)=a2﹣b2 B. (2x+1)(2x﹣1)=2x2﹣1
C. (x+1)(x﹣1)=x2﹣1 D. (﹣3x+2)(﹣3x﹣2)=9x2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C-∠B=30°,则∠DAE=________.
(3)若∠C-∠B=![]() (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
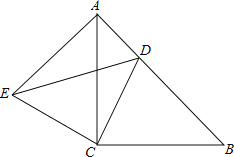
(1)试说明:∠EAC=∠B;
(2)若AD=10,BD=24,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
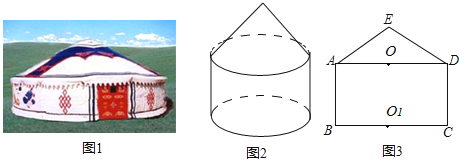
【题目】图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界文化遗产长城总长约6 700 000m,用科学记数法可表示为( )
A.6.7×105m B.6.7×10﹣5m
C.6.7×106m D.6.7×10﹣6m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com