
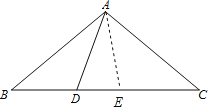
【题目】在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.

(1)若CD=CA=AB,请求出y与x的等量关系式;
(2)当D为边BC上一点,并且CD=CA,x=40,y=30时,则AB AC(填“=”或“≠”);
(3)如果把(2)中的条件“CD=CA”变为“CD=AB”,且x,y的取值不变,那么(1)中的结论是否仍成立?若成立请写出证明过程,若不成立请说明理由.
【答案】(1)3x+2y=180;(2)=;(3)成立.理由见解析
【解析】
试题分析:(1)由CD=CA,可表示出∠ADC的度数,又由三角形外角的性质,可得∠ADC=∠B+∠BAD,则可得方程:90﹣![]() x=x+y,继而求得答案;
x=x+y,继而求得答案;
(2)由CD=CA,x=40,y=30,首先可求得∠ADC的度数,继而证得CD=CA,则可求得∠C=∠B=40°,证得AB=AC;
(3)首先在BC上取点E,使BE=CD=AB,连接AE,易证得AD=AE,继而可得△ADB≌△AEC(SAS),则可证得结论.
解:(1)∵∠ABC=x°,CA=AB,
∴∠C=∠ABC=x°,
∵CD=CA,
∴∠ADC=∠CAD=![]() =90°﹣
=90°﹣![]() x°,
x°,
∵∠ADC=∠B+∠BAD,
∴90﹣![]() x=x+y,
x=x+y,
即:3x+2y=180;
(2)∵CD=CA,∠ABC=x°=40°,∠BAD=y°=30°,
∴∠ADC=∠ABC+∠BAD=70°,
∵CD=CA,
∴∠CAD=∠CDA=70°,
∴∠C=40°,
∴∠C=∠ABC,
∴AB=AC;
故答案为:=;
(3)成立.
理由:在BC上取点E,使BE=CD=AB,连接AE,
则∠AEB=∠EAB=![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∴∠AEB=∠ADE=70°,
∴AD=AE,
∴∠ADB=∠AEC=180°﹣70°=110°,
∵BD=BE﹣DE,CE=CD﹣DE,
∴BD=EC,
在△ADB和△AEC中,
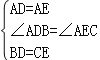 ,
,
∴△ADB≌△AEC(SAS),
∴AB=AC.


科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
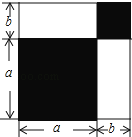
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某计算装置有一数据的入口A和一运算结果的出口B.
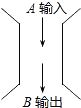
下表是小刚输入一些数后所得的结果:
![]()
(1)若输出的数是5,则小刚输入的数是多少?
(2)若小刚输入的数是225,则输出的结果是多少?
(3)若小刚输入的数是n(n≥10),你能用含n的式子表示输出的结果吗?试一试.
查看答案和解析>>
科目:初中数学 来源: 题型:
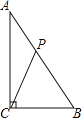
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
A.5 B.5或8 C.![]() D.4或
D.4或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
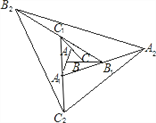
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
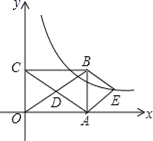
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com