
【题目】如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E
(1)试说明:BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果;
(3)若直线AE绕A点旋转到图(3)位置时(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不需说明理由.

【答案】(1)证明见解析;(2)DE=BD+CE;(3)DE=BD+CE.
【解析】试题分析:(1)证明△ABD≌△CAE,即可证得BD=AE,AD=CE,而AE=AD+DE=CE+DE,即可证得;
(2)(3)图形变换了,但是(1)中的全等关系并没有改变,因而BD与DE、CE的关系并没有改变.
解:(1)证明:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∠BAD+∠ABD=90°,
∴∠ABD=∠EAC,
又∵AB=AC,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AE=AD+DE=CE+DE,
∴BD=DE+CE.
(2)同理可得,DE=BD+CE;
(3)同理可得,DE=BD+CE.


科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙二人在环形跑道上同时同地出发,同向跑步,甲的速度为7米/秒,乙的速度为6.5米/秒,若跑道一周的长为400米,设经过x秒后甲乙两人第一次相遇,则列方程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
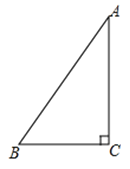
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹:
①作∠ACB的平分线,交斜边AB于点D;
②过点D作AC的垂线,垂足为点E.
(2)在(1)作出的图形中,若CB=6,DE=4,则△BCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
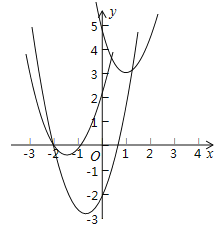
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com