
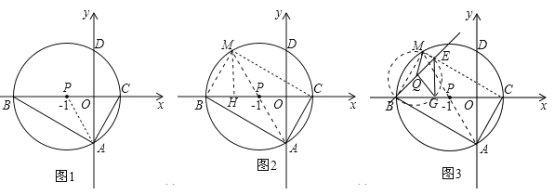
����Ŀ����ͼ���Ե�P��-1,0��ΪԲ�ĵ�Բ����x����B��C���㣨B��C����ࣩ����y����A��D���㣨A��D���·�����AD=![]() ������ABC�Ƶ�P��ת180�����õ���MCB��
������ABC�Ƶ�P��ת180�����õ���MCB��

��1����B��C��������ꣻ
��2������ͼ�л����߶�MB��MC�����ж��ı���ACMB����״������֤�����������M�����ꣻ
��3����ֱ��l����BM�غϵ�λ�ÿ�ʼ�Ƶ�B˳ʱ����ת������BC�غ�ʱֹͣ����ֱ��l��CM����ΪE����QΪBE���е㣬����E��EG��BC��G������MQ��QG����������ת�����С�MQG�Ĵ�С�Ƿ�仯�������䣬�����MQG�Ķ��������仯����˵�����ɣ�
���𰸡���1��B����3��0����C��1��0������2�����Σ�M������Ϊ����2��![]() ������3������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����
������3������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����
�������������������1������PA�����ô������������ɶ����������Բ�İ뾶���Ӷ��������B��C��������꣮
��2������ԲP�����ĶԳ�ͼ�Σ���Ȼ����AP��ԲP�Ľ���������軭�ĵ�M������MB��MC���ɣ���֤�ı���ACMB�Ǿ��Σ�����M��MH��BC������ΪH����֤��MHP�ա�AOP���Ӷ����MH��OH�ij��������õ���M�����꣮
��3����֤��E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ�ϣ��Ӷ��õ���MQG=2��MBG������OCA=60�����Ӷ��õ���MBG=60���������õ���MQG=120����������MQG�Ƕ�ֵ��
����������⣺��1������PA����ͼ1��ʾ����PO��AD����AO=DO����AD=![]() ����OA=
����OA=![]() ������P��������1��0������OP=1����PA=
������P��������1��0������OP=1����PA=![]() =2����BP=CP=2����B����3��0����C��1��0����
=2����BP=CP=2����B����3��0����C��1��0����
��2������AP���ӳ�AP����P�ڵ�M������MB��MC����ͼ2��ʾ���߶�MB��MC��Ϊ���������ı���ACMB�Ǿ��Σ��������£�
�ߡ�MCB����ABC�Ƶ�P��ת180�����ã����ı���ACMB��ƽ���ı��Σ�
��BC����P��ֱ�������CAB=90������ƽ���ı���ACMB�Ǿ��Σ�
����M��MH��BC������ΪH����ͼ2��ʾ��
����MHP����AOP�У��ߡ�MHP=��AOP����HPM=��OPA��MP=AP�����MHP�ա�AOP����MH=OA=![]() ��PH=PO=1����OH=2������M������Ϊ����2��
��PH=PO=1����OH=2������M����������2��![]() ����
����
��3������ת��������MQG�Ĵ�С���䣮
���ı���ACMB�Ǿ��Σ����BMC=90������EG��BO�����BGE=90�������BMC=��BGE=90����
����Q��BE���е㣬��QM=QE=QB=QG������E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ�ϣ���ͼ3��ʾ�����MQG=2��MBG���ߡ�COA=90����OC=1��OA=![]() ����tan��OCA=
����tan��OCA=![]() =
=![]() �����OCA=60�������MBC=��BCA=60�������MQG=120����������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����
�����OCA=60�������MBC=��BCA=60�������MQG=120����������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
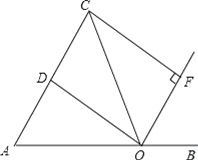
����Ŀ����ͼ����O���߶�AB�ϵ�һ�㣬OA=OC��ODƽ�֡�AOC��AC�ڵ�D��OFƽ�֡�COB��CF��OF�ڵ�F��
��1����֤���ı���CDOF�Ǿ��Σ�
��2������AOC���ٶ�ʱ���ı���CDOF�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����������۲�ͬ���¾�����80Ԫ��һ��ӯ��60%����һ������20%������������̼ң�������
A. ���ⲻ B. ��10Ԫ C. �ˣ�Ԫ D. ��32Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ķ���:����������������ͽ��۸պ��෴,��ô�����������������,���������һ���������ԭ����,��ô��һ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A(x1��y1)��B(x2��y2)����ֱ��y��kx+2��k��0���ϣ���x1��x2��y1��y2�Ĵ�С��ϵ�ǣ� ��
A.y1 ��y2B.y1 ��y2C.y1 ��y2D.y1 ��y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��E��F��C��һ��ֱ���ϣ�AE=CF����E��F�ֱ���DE��AC��B F��AC����AB=CD��
��1��ͼ����������������ȫ�������Σ���������д������
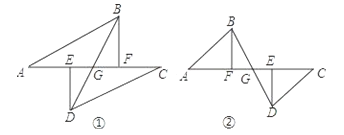
��2����֤��G��BD���е㣮
��3��������ABF�ı�AF��GA�����ƶ���Ϊͼ��ʱ�������������䣬�ڣ�2�����еĽ����Ƿ�������������������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������֪��ABC�У���BAC=90����AB=AC��AE�ǹ�A��һ��ֱ�ߣ���B��C��A��E����࣬BD��AE��D��CE��AE��E
��1����˵����BD=DE+CE��
��2����ֱ��AE��A����ת��ͼ��2��λ��ʱ��BD��CE���������������䣬��BD��DE��CE�Ĺ�ϵ��Σ���ֱ��д�������
��3����ֱ��AE��A����ת��ͼ��3��λ��ʱ��BD��CE���������������䣬��BD��DE��CE�Ĺ�ϵ��Σ���ֱ��д�����������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
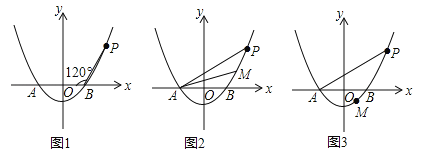
����Ŀ����֪������![]() ��a��0����x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����P����������һ�㣬��PB=AB����PBA=120�㣬��ͼ��ʾ��
��a��0����x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����P����������һ�㣬��PB=AB����PBA=120�㣬��ͼ��ʾ��
��1���������ߵĽ���ʽ��
��2�����M��m��n��Ϊ�������ϵ�һ�����㣬��������PA���ƶ���
�ٵ���M������PB֮�䣨���˵㣩�ƶ�ʱ���Ƿ���ڵ�Mʹ��APM�����Ϊ![]() �������ڣ����M�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ����M�����ꣻ�������ڣ���˵�����ɣ�
�ڵ���M������BA֮�䣨���˵㣩�ƶ�ʱ����|m|+|n|�����ֵ��ȡ�����ֵʱ��M�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com