
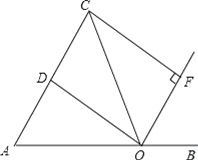
【题目】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
【答案】(1)证明见解析(2)当∠AOC=90°时,四边形CDOF是正方形,理由见解析
【解析】(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),
∴∠AOC=2∠COD,∠COB=2∠COF。
∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°。∴∠COD+∠COF=90°。
∴∠DOF=90°。
∵OA=OC,OD平分∠AOC(已知)。
∴OD⊥AC,AD=DC(等腰三角形的“三合一”的性质)。∴∠CDO=90°。
∵CF⊥OF,∴∠CFO=90°。
∴四边形CDOF是矩形。
(2)解:当∠AOC=90°时,四边形CDOF是正方形。理由如下:
∵∠AOC=90°,AD=DC,∴OD=DC。
又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形。
因此,当∠AOC=90°时,四边形CDOF是正方形。
(1)利用角平分线的性质、平角的定义可以求得∠DOF=90°;由等腰三角形的“三合一”的性质可推知OD⊥AC,即∠CDO=90°;根据已知条件“CF⊥OF”知∠CFO=90°;则三个角都是直角的四边形是矩形。
(2)当∠AOC=90°时,四边形CDOF是正方形;因为Rt△AOC的斜边上的中线OD等于斜边的一半,所以矩形的邻边OD=CD,所以矩形CDOF是正方形。


科目:初中数学 来源: 题型:
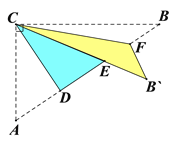
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CD翻折,使点A落在AB上的点E处;再将边BC沿CF翻折,使点B落在CE的延长线上的点B′处,两条折痕与斜边AB分别交于点D、F,则线段B′F的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了分析全市1万名初中毕业生的数学毕业成绩,共随机抽取40本试卷,每本30份,则这个问题中( )
A.个体是每个学生
B.样本是抽取的1200名学生的数学毕业成绩
C.总体是40本试卷的数学毕业成绩
D.样本是30名学生的数学毕业成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
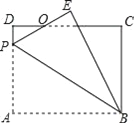
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com