
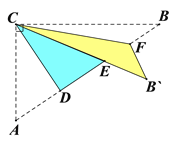
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CD翻折,使点A落在AB上的点E处;再将边BC沿CF翻折,使点B落在CE的延长线上的点B′处,两条折痕与斜边AB分别交于点D、F,则线段B′F的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】首先根据折叠可得CD=AC=3,BC=4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,然后求得△BCF是等腰直角三角形,进而求得∠B/GD=90°,CE-EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
从而求得B/D=1,DF=![]() ,在Rt△B/DF中,由勾股定理即可求得B/F的长.
,在Rt△B/DF中,由勾股定理即可求得B/F的长.
解:根据首先根据折叠可得CD=AC=3,B/C=B4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,
∴BD=4-3=1,∠DCE+∠B/CF=∠ACE+∠BCF,
∴∠ACB=90°,∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B/FC=135°,
∴∠B/FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,∴EF=
,∴EF=![]() ,ED=AE=
,ED=AE=![]() =
=![]()
∴DE=EF-ED=![]() ,
,
∴B/F=![]() =
=![]() .
.
故答案为:![]()
“点睛”此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等,根据折叠的性质求得相等的角是解本题的关键.


科目:初中数学 来源: 题型:
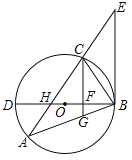
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016四川省凉山州)阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为a,b,c,记![]() ,那么三角形的面积为
,那么三角形的面积为![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: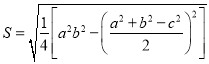 . ②
. ②
下面我们对公式②进行变形: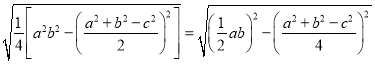
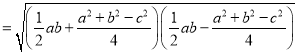
![]()
![]()
![]()
![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
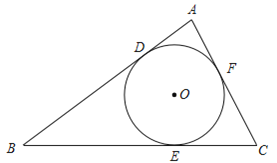
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台市通过扩消费、促投资、稳外需的协同发力,激发了区域发展活力,实现了经济平稳较快发展.2013年全市生产总值(GDP)达5 613亿元.该数据用科学记数法表示为( )
A.5.613×1011元B.5.613×1012元
C.56.13×1010元D.0.561 3×1012元
查看答案和解析>>
科目:初中数学 来源: 题型:
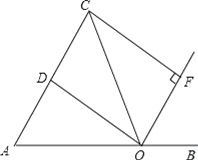
【题目】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com