
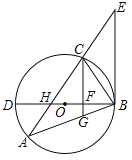
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.
(2)由△ABC∽△CBG,得![]() 求出BC,再由△BFC∽△BCD,得
求出BC,再由△BFC∽△BCD,得![]() =BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
=BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
试题解析:(1)连接CD,∵BD是直径,∴∠BCD=90°,即∠D+∠CBD=90°,∵∠A=∠D,∠A=∠EBC,∴∠CBD+∠EBC=90°,∴BE⊥BD,∴BE是⊙O切线.
(2)∵CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,∵∠CBG=∠ABC
∴△ABC∽△CBG,∴![]() ,即
,即![]() =BGBA=48,∴BC=
=BGBA=48,∴BC=![]() ,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴
,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴![]() =BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=
=BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=![]() =
=![]() ,∴CG=CF+FG=
,∴CG=CF+FG=![]() ,在RT△BFG中,BG=
,在RT△BFG中,BG=![]() =
=![]() ,∵BGBA=48,∴BA=
,∵BGBA=48,∴BA=![]() ,即AG=
,即AG=![]() ,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=
,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=![]() ,∵△ABC∽△CBG,∴
,∵△ABC∽△CBG,∴![]() ,∴AC=
,∴AC=![]() =
=![]() ,∴AH=AC﹣CH=
,∴AH=AC﹣CH=![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CD翻折,使点A落在AB上的点E处;再将边BC沿CF翻折,使点B落在CE的延长线上的点B′处,两条折痕与斜边AB分别交于点D、F,则线段B′F的长为( )
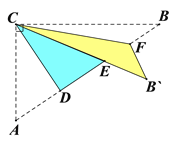
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了分析全市1万名初中毕业生的数学毕业成绩,共随机抽取40本试卷,每本30份,则这个问题中( )
A.个体是每个学生
B.样本是抽取的1200名学生的数学毕业成绩
C.总体是40本试卷的数学毕业成绩
D.样本是30名学生的数学毕业成绩
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com