
【题目】解不等式组: 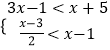 并写出它的整数解.
并写出它的整数解.
【答案】解:解不等式3x﹣1<x+5,得:x<3,
解不等式 ![]() <x﹣1,得:x>﹣1,
<x﹣1,得:x>﹣1,
则不等式组的解集为﹣1<x<3,
∴不等式组的整数解为0、1、2.
【解析】解不等式组的基本步骤是移项、合并同类项,两边同时除以一次项系数(负数时要改变不等式方向)分别解出两个不等式, 求出它们的公共部分,再找出整数解.
【考点精析】利用一元一次不等式组的解法和一元一次不等式组的整数解对题目进行判断即可得到答案,需要熟知解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2,例如二次三项式x2-2x+9的配方过程如下:x2-2x+9=x2-2x+1-1+9=(x-1)2+8.
请根据阅读材料解决下列问题:
(1)比照上面的例子,将下面的两个二次三项式分别配方:
①x2-4x+1=______;
②3x2+6x-9=3(x2+2x)-9=______;
(2)已知x2+y2-6x+10y+34=0,求3x-2y的值;
(3)已知a2+b2+c2+ab-3b+2c+4=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
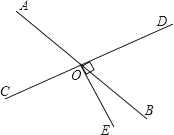
【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=![]() ∠AOC,
∠AOC,
(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于![]() 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,引射线OC(点C在∠AOB外),OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=40°,请依题意补全图,并求∠BOE的度数;
(2)若∠BOC=α(0°<α<180°),请直接写出∠BOE的度数(用含α的代数式表示).
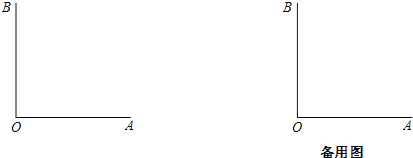
查看答案和解析>>
科目:初中数学 来源: 题型:
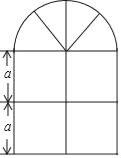
【题目】如图,某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆内部用了三根等长的木条分隔,下部是用木条围成的边长相同的四个小正方形,木条宽厚不计,已知下部的小正方形的边长为a米.
(1)用含a的式子分别表示窗户的面积和木条用料(实线部分)的总长;
(2)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,木条每米20元,求制作这扇窗户需要多少元?(π取3,结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
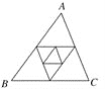
【题目】如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2 016个三角形的周长为( )
A. 22 016 B. 22 017 C. (![]() )2 016 D. (
)2 016 D. (![]() )2 015
)2 015
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com