
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.

【答案】扩充后的等腰三角形绿地的周长为32m或(20+4![]() )m或
)m或 ![]() m.
m.
【解析】试题分析:根据题意画出图形,构造出等腰三角形,根据等腰三角形及直角三角形的性质利用勾股定理解答即可.
试题解析:在Rt△ABC中,∠ACB=90°,AC=8m,BC=6m,由勾股定理有:AB=10m,应分以下三种情况:
①如图1,
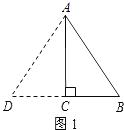
当AB=AD=10m时,
∵AC⊥BD,
∴CD=CB=6m,
∴△ABD的周长=10+10+2×6=32(m).
②如图2,
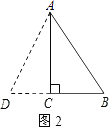
当AB=BD=10m时,
∵BC=6m,
∴CD=10﹣6=4m,
∴AD= ![]() =
=![]() =4
=4![]() (m),
(m),
∴△ABD的周长=10+10+4![]() =(20+4
=(20+4![]() )m.
)m.
③如图3,
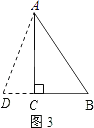
当AB为底时,设AD=BD=x,则CD=x﹣6,
∵由勾股定理得:AD2=AC2+CD2=82+(x﹣6)2=x2 ,
解得x=![]() ,
,
∴△ABD的周长为:AD+BD+AB=![]() +
+ ![]() +10=
+10= ![]() (m).
(m).
综上所述,扩充后的等腰三角形绿地的周长为:32m或(20+4![]() )m或
)m或 ![]() m.
m.


科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB=_____ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一次函数y=﹣x+b与反比例函数y= ![]() (k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y=
(k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y= ![]() (k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.
(k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.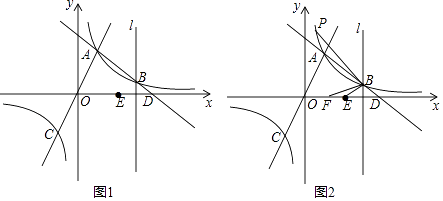
(1)k=;
(2)判断点B,E,C是否在同一条直线上,并说明理由;
(3)如图2,已知点F在x轴正半轴上,OF= ![]() ,点P是反比例函数y=
,点P是反比例函数y= ![]() (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).
(k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )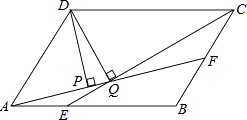
A.3:4
B.![]() :2
:2 ![]()
C.![]() :2
:2 ![]()
D.2 ![]() :
: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
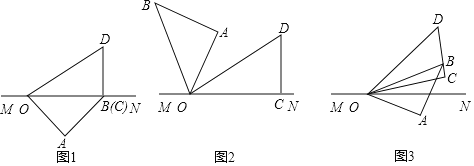
【题目】将一副三角板如图1摆放在直线MN上,在三角板OAB和三角板OCD中,![]() ,
,![]() ,
,![]() .
.
![]() 保持三角板OCD不动,将三角板OAB绕点O以每秒
保持三角板OCD不动,将三角板OAB绕点O以每秒![]() 的速度逆时针旋转,旋转时间为t秒.
的速度逆时针旋转,旋转时间为t秒.
![]() 当
当![]() ______秒时,OB平分
______秒时,OB平分![]() 此时
此时![]() ______
______![]() ;
;
![]() 当三角板OAB旋转至图2的位置,此时
当三角板OAB旋转至图2的位置,此时![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
![]() 如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒
如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒![]() 的速度逆时针旋转,当OB旋转至射线OM上时同时停止.
的速度逆时针旋转,当OB旋转至射线OM上时同时停止.
![]() 当t为何值时,OB平分
当t为何值时,OB平分![]() ?
?
![]() 直接写出在旋转过程中,
直接写出在旋转过程中,![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com