
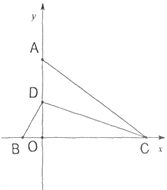
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

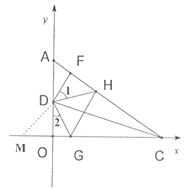
(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
【答案】(1)证明见解析;(2)8;(3)GH=FH+OG,证明见解析.
【解析】试题分析: (1)由题意∠CAO=90°-∠BDO,可知∠CAO=∠CBD,CD平分∠ACB与y轴交于D点,所以可由AAS定理证明△ACD≌△BCD,由全等三角形的性质可得AC=BC;
(2)过D作DN⊥AC于N点,可证明Rt△BDO≌Rt△EDN、△DOC≌△DNC,因此,BO=EN、OC=NC,所以,BC+EC=BO+OC+NC-NE=2OC,即可得BC+EC的长;
(3)在x轴的负半轴上取OM=FH,可证明△DFH≌△DOM、△HDG≌△MDG,因此,MG=GH,所以,GH=OM+OG=FH+OG,即可证明所得结论.
试题解析:
(1)证明:∵∠CAO=90°-∠BDO,
∴∠CAO=∠CBD.
又∵∠ACD=∠BCD,CD=CD,
∴△ACD≌△BCD(AAS).
∴AC=BC.
(2)解:过D作DN⊥AC于N点,如图所示:
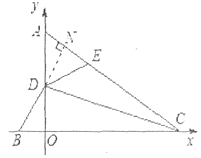
∵∠ACD=∠BCD,∠DOC=∠DNC=90°,
CD=CD
∴△DOC≌△DNC(AAS),
∴DO=DN,OC=NC.
又∵∠DEA=∠DBO,∠DOB=∠DNC=90°
∴△BDO≌△EDN(AAS),
∴BO=EN.
∴BC+EC=BO+OC+NC-NE=2OC=8.
(3)GH=FH+OG.
证明:由(1)知:DF=DO,
在x轴的负半轴上取OM=FH,连接DM,
如图所示:
在△DFH和△DOM中
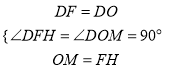
∴△DFH≌△DOM(SAS).
∴DH=DM,∠l=∠ODM.
∴∠GDH=∠1+∠2=∠ODM+∠2=∠GDM.
在△HDG和△MDG中
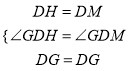
∴△HDG≌△MDG(SAS).
∴MG=GH,
∴GH=OM+OG=FH+OG.
点睛: 本题主要考查了全等三角形的判定及其性质,做题时添加了辅助线,正确作出辅助线是解决问题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
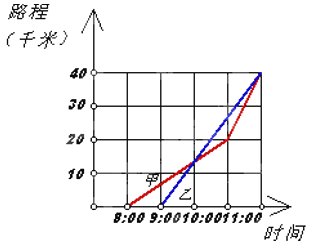
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
(5)你能将图象中得到信息,编个故事吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | 94 | b | 93 | 12 |
九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(1)直接写出表中a、b的值:a= , b=;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE。F为AB上一点,且BF=DE,连接FC.
(1)若DE=1,CF=2![]() ,求CD的长。
,求CD的长。
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=600,求证:AF+CE=![]() AC.
AC.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() 射线
射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转,射线
便立即逆时针回转,射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转.射线
便立即逆时针回转.射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度,射线
度,射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度.
度.

(1)直接写出![]() 的大小为_______;
的大小为_______;
(2)射线![]() 、
、![]() 转动后对应的射线分别为
转动后对应的射线分别为![]() 、
、![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,若射线
,若射线![]() 比射线
比射线![]() 先转动
先转动![]() 秒,设射线
秒,设射线![]() 转动的时间为
转动的时间为![]()
![]() 秒,求
秒,求![]() 为多少时,直线
为多少时,直线![]() 直线
直线![]() ?
?
(3)如图2,若射线![]() 、
、![]() 同时转动
同时转动![]()
![]() 秒,转动的两条射线交于点
秒,转动的两条射线交于点![]() ,作
,作![]() ,点
,点![]() 在
在![]() 上,请探究
上,请探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过独立思考与分析后,小明和小聪开始交流解题思路如下:
小明说:解这个关于x的分式方程,得到方程的解为![]() .由题意可得
.由题意可得![]() ,所以
,所以![]() ,问题解决.
,问题解决.
小聪说:你考虑的不全面.还必须保证![]() 才行.
才行.
请回答:_______________的说法是正确的,并说明正确的理由是:__________________.
完成下列问题:
(1)已知关于x的方程![]() 的解为非负数,求m的取值范围;
的解为非负数,求m的取值范围;
(2)若关于x的分式方程![]() 无解.直接写出n的取值范围.
无解.直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com