
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE。F为AB上一点,且BF=DE,连接FC.
(1)若DE=1,CF=2![]() ,求CD的长。
,求CD的长。
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=600,求证:AF+CE=![]() AC.
AC.


【答案】(1)3;(2)见解析.
【解析】分析:(1)先证明△ADE≌△CBF,可得AE=CF=![]() ,设CD=x,则CE=AC=x+1 ,在Rt△ACD中根据勾股定理列方程求解;
,设CD=x,则CE=AC=x+1 ,在Rt△ACD中根据勾股定理列方程求解;
(2)延长BG交CD的延长线于点M,先证明△ABG≌EMG,从而可得CE+AF= 2CD,由等腰三角形的性质和三角形外角的性质可求∠M=∠MCG=∠ACG=∠ABG=15°,从而∠ACD=30,由cos∠ACD=![]() 得
得![]() ,进而可证明结论.
,进而可证明结论.
详解:(1)解:∵矩形ABCD ,
∴AD=BC,∠ADC=∠ABC=90 .
∵∠ADE+∠ADC=180 ,
∴∠ADC=90 ,
∴∠ADC=∠ABC .
∵BF=DE ,
∴△ADE≌△CBF ,
∴AE=CF=![]() ,
,
∴在Rt△ABC中,
AD=![]() ,
,
设CD=x,则CE=AC=x+1 ,
![]() ,
,
解得:![]() ,
,
即:![]() ;
;
(2)证明:延长BG交CD的延长线于点M
易证△ABG≌EMG,
∴GM=GB,AB=CD,∠ABG=∠M,
又BF=ED,
∴AF=ME.
∴CE+AF=CE+ME=2CD,
连接CG, 在Rt△MCB,
CG=MG,
∴∠M=∠MCG.
又CA=CE,且点G是AE的中点,
∴ ∠MCG=∠ACG,
又∠BHC=∠M+∠MCG+∠ACG, ∠BHC+∠ABG=60,
∴∠M=∠MCG=∠ACG=∠ABG=15
∴∠ACD=30
∵cos∠ACD=![]() ,
,
∴![]() ,
,
∴AF+CE=![]() AC.
AC.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.有以下说法:①小文同学一共统计了60人;②每天微信阅读不足20分钟的人数有8人;③每天微信阅读30~40分钟的人数最多;④每天微信阅读0-10分钟的人数最少.根据图中信息,上述说法中正确的是( )

A. ①②③④ B. ①②③ C. ②③④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB=_____ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )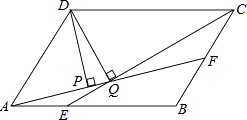
A.3:4
B.![]() :2
:2 ![]()
C.![]() :2
:2 ![]()
D.2 ![]() :
: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com