
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

【答案】见解析
【解析】
解:若△ABC为锐角三角形,则有a2+b2>c2,若△ABC为钝角三角形,∠C为钝角,则有a2+b2<c2.
证明:(1)当△ABC为锐角三角形时,过点A作AD⊥CB,垂足为D,设CD=x,则有DB=a-x.
根据勾股定理,得b2-x2=c2-(a-x)2,即b2-x2=c2-a2+2ax-x2.
∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,
∴a2+b2>c2.
(2)当△ABC为钝角三角形时,过B作BD⊥AC,交AC的延长线于点D,设CD=x,则BD2=a2-x2.根据勾股定理,得(b+x)2+(a2-x2)=c2,∴a2+b2+2bx=c2.
∵b>0,x>0,∴2bx>0,∴a2+b2<c2.



科目:初中数学 来源: 题型:
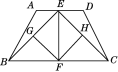
【题目】如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别为BE,BC,CE的中点.
(1)试说明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF=![]() BC,试说明平行四边形EGFH是正方形.
BC,试说明平行四边形EGFH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣ ![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.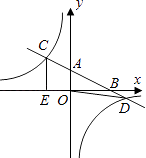
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
(3)x取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,时钟是我们常见的生活必需品,其中蕴含着许多数学知识.

(1)我们知道,分针和时针转动一周都是 度,分针转动一周是 分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动 度,时针每分钟转动 度.
(2)从5:00到5:30,分针与时针各转动了多少度?
(3)请你用方程知识解释:从1:00开始,在1:00到2:00之间,是否存在某个时刻,时针与分针在同一条直线上?若不存在,说明理由;若存在,求出从1:00开始经过多长时间,时针与分针在同一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试.某校对初三学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.小张同学对物理的①、②和化学的b、c实验准备得较好,请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )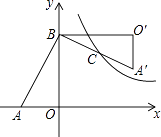
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com