
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
【答案】
(1)解:∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.
∴抛物线的表达式为y=x2+2x﹣3
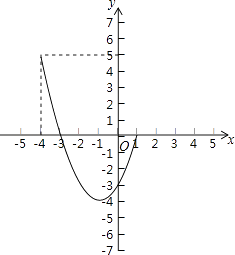
(2)解:y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.
∴﹣4<x<1时,y的取值范围是﹣4≤y<5
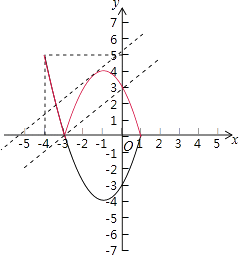
(3)解:y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).
新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b= ![]() .
.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b< ![]() .
.
【解析】(1)把点(1,0)代入抛物线解析式得到关于m的方程,从而可求得m的值,将m的值代入可得到抛物线的表达式;
(2)先求得抛物线的顶点坐标和对称轴,然后画出大致图像,最后,依据函数图像进行判断即可;
(3)根据题意作出函数图象,然后由函数图像可确定新图象M与直线有三个交点时的界点,然后利用待定系数法求解即可.
【考点精析】本题主要考查了二次函数的性质和二次函数图象的平移的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:
①1×3-22=3-4=-1;
②2×4-32=8-9=-1;
③3×5-42=15-16=-1;
…
(1)请按照以上规律写出第10个等式。
(2)请按照以上规律写出第n个等式。
(3)(2)中的式子一定成立吗?若不一定成立,请举出反例;若一定成立,请说出理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.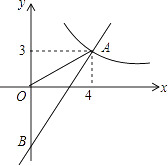
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
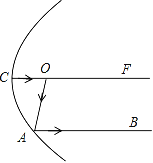
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气温随着高度的升高而下降,下降的一般规律是从地面到高空11 km处(包括11 km),每升高1 km气温下降6 ℃;高于11 km时,气温不再发生变化,地面的气温为20 ℃时,设高空中x km处的气温为y ℃.
(1)当0≤x≤11时,求y和x之间的关系式;
(2)画出气温随高度(包括高于11 km)变化的图像;
(3)在离地面4.5 km及14 km的高空处,气温分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=10,E为AB上一点,且AE= ![]() AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.
AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.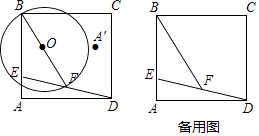
(1)用a的代数式表示DE2= , BF2=;
(2)求证:⊙O必过BC的中点;
(3)若⊙O与矩形ABCD各边所在的直线相切时,求a的值;
(4)作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com