
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.
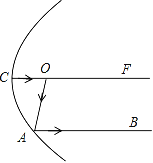
【答案】53°或97°
【解析】
分析题目,可知需分两种情况讨论,首先画出图形;
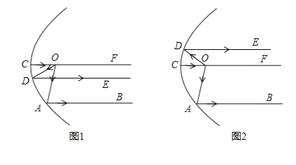
可知如果∠AOD是锐角,则∠AOD=∠COA-∠COD,如果∠AOD是钝角,则∠AOD=∠COA+∠COD;然后由平行线的性质求出∠COA,∠COD,从而求出∠AOD的度数.
分析题意,画出图形.

∵AB∥CF,
∴∠COA=∠OAB.
∵∠OAB=75°,
∴∠COA=75°.
∵DE∥CF,
∴∠COD=∠ODE.
∵∠ODE=22°,
∴∠COD=22°.
在图1的情况下,
∠AOD=∠COA-∠COD=75°-22°=53°.
在图2的情况下,
∠AOD=∠COA+∠COD=75°+22°=97°.
∴∠AOD的度数为53°或97°.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )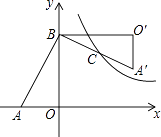
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,将□ABCD沿过点A的直线![]() 折叠,使点D落到AB边上的点
折叠,使点D落到AB边上的点![]() 处,折痕
处,折痕![]() 交CD边于点E,连接BE
交CD边于点E,连接BE
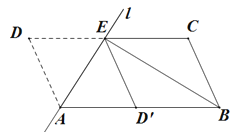
(1)求证:四边形![]() 是平行四边形
是平行四边形
(2)若BE平分∠ABC,求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程组:①![]() ②
②![]() ③
③![]() ④
④![]() ,比较适宜的方法是( )
,比较适宜的方法是( )
A.①②用代入法,③④用加减法B.①③用代入法,②④用加减法
C.②③用代入法,①④用加减法D.②④用代入法,①③用加减法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:①以点A为圆心,适当长为半径画弧,
交直线BC于点M,N;
②分别以点M,N为圆心,以大于![]() MN的长为半径画弧,两弧相交于点P;
MN的长为半径画弧,两弧相交于点P;
③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵AM= ,MP= ,
∴AP是线段MN的垂直平分线.( )(填推理的依据)
∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com