
【题目】(本题满分10分)如图,将□ABCD沿过点A的直线![]() 折叠,使点D落到AB边上的点
折叠,使点D落到AB边上的点![]() 处,折痕
处,折痕![]() 交CD边于点E,连接BE
交CD边于点E,连接BE
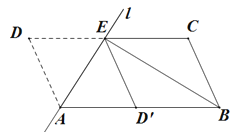
(1)求证:四边形![]() 是平行四边形
是平行四边形
(2)若BE平分∠ABC,求证:![]()
【答案】见解析
【解析】试题(1)根据翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,然后根据平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;
(2)根据平行线的性质利用勾股定理得出答案.
试题解析:(1)∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,∴∠DEA=∠EAD′,∴∠DAE=∠EAD′=∠DEA=∠D′EA,∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,∴DE=AD′,
∵四边形ABCD是平行四边形,∴AB![]() DC,∴CE
DC,∴CE![]() D′B,∴四边形BCED′是平行四边形;
D′B,∴四边形BCED′是平行四边形;
(2)∵BE平分∠ABC,∴∠CBE=∠EBA,
∵AD∥BC,∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,∴∠EAB+∠EBA=90°,∴∠AEB=90°,∴AB2=AE2+BE2.


科目:初中数学 来源: 题型:
【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由.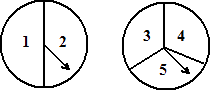
查看答案和解析>>
科目:初中数学 来源: 题型:
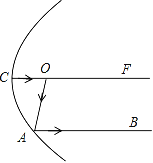
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图像大致为( )
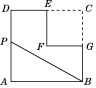
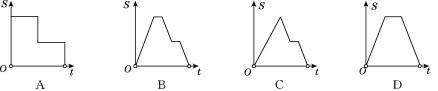
A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.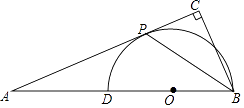
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com