
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

【答案】(1)见解析;(2)BD=DE+CE,理由见解析.
【解析】
(1)先证△AEC≌△BDA得出AD=CE,BD=AE,从而得出DE=BD+CE;
(2)先证△ADB≌△CEA得出AD=CE,BD=AE,从而得出BD=DE+CE.
(1)∵BD⊥DE,CE⊥DE,∴∠D=∠E=90°,∴∠DBA+∠DAB=90°.
∵∠BAC=90°,∴∠DAB+∠CAE=90°,∴∠DBA=∠CAE.
∵AB=AC,∴△ADB≌△CEA,∴BD=AE,CE=AD,∴DE=AD+AE=CE+BD;
(2)BD=DE+CE.理由如下:
∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°,∴∠ABD+∠BAD=90°.
∵∠BAC=90°,∴∠ABD+∠EAC=90°,∴∠BAD=∠EAC.
∵AB=AC,∴△ADB≌△CEA,∴BD=AE,CE=AD.
∵AE=AD+DE,∴BD=CE+DE.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
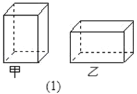
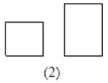
【题目】某纸品加工厂利用边角料裁出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图2),再将它们制作成甲乙两种无盖的长方体小盒(如图1).现将300张长方形硬纸片和150张正方形硬纸片全部用于制作这两种小盒,可以做成甲乙两种小盒各多少个?(注:图1中向上的一面无盖)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.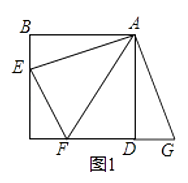
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
(1)【类比引申】如图2,点E,F分别在正方形ABCD的边CB,CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF,BE,DF之间的数量关系,并证明;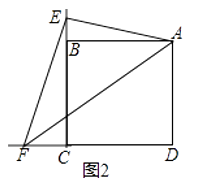
(2)【联想拓展】如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.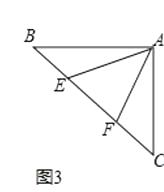
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,将□ABCD沿过点A的直线![]() 折叠,使点D落到AB边上的点
折叠,使点D落到AB边上的点![]() 处,折痕
处,折痕![]() 交CD边于点E,连接BE
交CD边于点E,连接BE
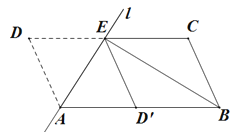
(1)求证:四边形![]() 是平行四边形
是平行四边形
(2)若BE平分∠ABC,求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.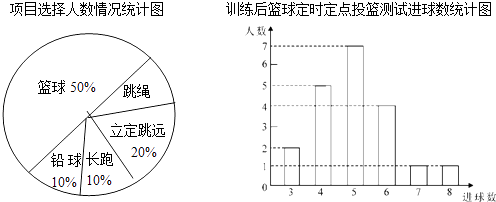
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
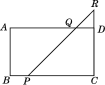
【题目】如图,在长方形ABCD中,AB=4,BC=7,点P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点R,交AD于点Q(点Q与点D不重合),且∠RPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:

(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是两位同学的一段对话:
聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.
明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.
聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.
根据对话内容,请你求出公交车和地铁的平均行驶速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com