
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】
利用边角边即可证明△ACE与△DCB全等,然后根据全等三角形对应角相等可得∠CAM=∠CDN,再利用角边角证明△ACM≌△DCN,根据全等三角形对应边相等可得CM=CN,DN=AM,同理可证明△BCN≌△ECM,根据全等三角形对应边相等可得BN=EM,根据三角形面积公式求出CQ=CH,即可判断④,根据三角形外角性质推出∠APD=60°.
∵△DAC和△EBC都是等边三角形,
∴∠ACD=∠BCE=60°,
∴∠ACE=∠DCB=120°,
在△ACE与△DCB中,
AC=DC,∠ACE=∠DCB,CB=CE,
∴△ACE≌△DCB(SAS),故①正确;
∴∠CAM=∠CDN,
在△ACM与△DCN中
∠CAM=∠CDN,AC=DC,∠ACM=∠DCN=60°,
∴△ACM≌△DCN(ASA),
∴CM=CN,故②正确;
DN=AM,
在△AMC中,AC>AM,
∴AC≠DN,故③错误;
过C作CQ⊥DB于Q,CH⊥AE于H,
∵△ACM≌△DCN,
∴△ACM和△DCN的面积相等,
∵DN=AM,
∴由三角形面积公式得:CQ=CH,
∴CP平分∠APB,∴④正确;
∵△ACE≌△DCB,
∴∠AEC=∠DBC,
∵∠ECB=60°,
∴∠EAC+∠AEC=∠ECB=60°,
∴∠APD=∠EAC+∠ABP=∠EAC+∠AEC=60°
∴⑤正确;
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.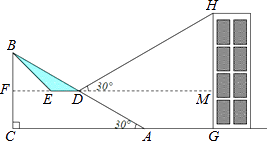
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
(1)求线段MN的长.
(2)当C在AB延长线上时,其他条件不变,求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
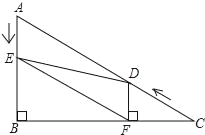
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由.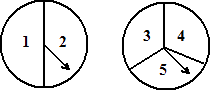
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com