练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为方便市民通行，某广场计划对坡角为30°，坡长为60米的斜坡AB进行改造，在斜坡中点D处挖去部分坡体（阴影表示），修建一个平行于水平线CA的平台DE和一条新的斜坡BE．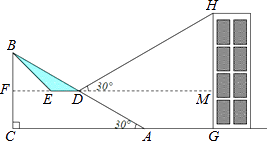

    【答案】
    【解析】（1）根据斜坡BE的坡角可知∠BEF=36°，再由∠DAC=∠BDF=30°，可得BF的长，在Rt△BEF中可求得出EF的长，再由DE=DF-EF可求得DE的长；
    （2）过点D作DP⊥AC，垂足为P，在Rt△DPA中，以及PA=AD·cos30°，进而得出DM的长，利用HM=DM·tan30°可求得.
    【考点精析】根据题目的已知条件，利用关于坡度坡角问题的相关知识可以得到问题的答案，需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

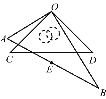
    【题目】将一副三角板按如图所示的方式叠放在一起,两直角顶点重合于点O.

    (1)求∠AOD+∠BOC的度数;

    (2)当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，，，，，，，，……

    (1)请你据此推测出的个位数字是几？

    (2)利用上面的结论，求的个位数字．

    (3)的个位数字又是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某人去水果批发市场采购猕猴桃，他看中了A、B两家猕猴桃．这两家猕猴桃品质一样，零售价都为6元／千克，批发价各不相同，

    A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．

    B家的规定如下表：

    数量范围

    （千克）

    0～500

    500以上～1500

    1500以上～2500

    2500以上

    价格（元）

    零售价的95%

    零售价的85%

    零售价的75%

    零售价的70%

    （1）如果他批发600千克猕猴桃，则他在A 、B两家批发分别需要多少元？

    （2）如果他批发x千克猕猴桃(1500＜x＜2000)，请你分别用含x的代数式表示他在A、B两家批发所需的费用；

    （3）现在他要批发1800千克猕猴桃，你能帮助他选择在哪家批发更优惠吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，圆柱底面半径为cm，高为9cm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一根棉线从A点顺着圆柱侧面绕3圈到B点，则这根棉线的长度最短为（ ）

    A. 12cm B. cm C. 15cm D. cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线AB交x轴于点A（5，0），交y轴于点B，AO是⊙M的直径，其半圆交AB于点C，且AC=3．取BO的中点D，连接CD、MD和OC．

    （1）求证：CD是⊙M的切线；
    （2）二次函数的图象经过点D、M、A，其对称轴上有一动点P，连接PD、PM，求△PDM的周长最小时点P的坐标；
    （3）在（2）的条件下，当△PDM的周长最小时，抛物线上是否存在点Q，使S△QAM= S△PDM？若存在，求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 1，在平面直角坐标系中，点 A 为 x 轴负半轴上一点，点 B 为 x 轴正半轴上一点，C（0，﹣2），D（﹣3，﹣2）．

    （1）AB，CD 的位置关系为 ；△BCD 的面积为 ；S△ACD S△BCD（填两者之间的数量关系）；

    （2）如图 1，若∠1=100°，∠ACB=65°，求∠CAB 的度数；

    （3）如图 2，若∠ADC=∠DAC，∠ACB 的平分线 CE 交 DA 的延长线于点 E，在 B 点的运动过程中的值是否变化？若不变，直接写出其值；若变化，请说明理由．（注：三角形内角和等于 180°）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

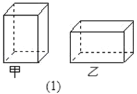
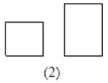
    【题目】某纸品加工厂利用边角料裁出正方形和长方形两种硬纸片，长方形的宽与正方形的边长相等（如图2），再将它们制作成甲乙两种无盖的长方体小盒（如图1）．现将300张长方形硬纸片和150张正方形硬纸片全部用于制作这两种小盒，可以做成甲乙两种小盒各多少个？（注：图1中向上的一面无盖）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，且A、C、B在同一直线上，有如下结论：①△ACE≌△DCB；②CM＝CN；③AC＝DN；④PC平分∠APB；⑤∠APD＝60°，其中正确结论有（　　）

    A. 5个 B. 4个 C. 3个 D. 2个

    查看答案和解析>>

    同步练习册答案