
【题目】某人去水果批发市场采购猕猴桃,他看中了A、B两家猕猴桃.这两家猕猴桃品质一样,零售价都为6元/千克,批发价各不相同,
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围 (千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发600千克猕猴桃,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克猕猴桃(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克猕猴桃,你能帮助他选择在哪家批发更优惠吗?请说明理由.
【答案】(1)A家:3312元,B家:3360元;(2)A家:![]() ;B家:
;B家:![]() ;(3)选择B家更优惠,理由见解析
;(3)选择B家更优惠,理由见解析
【解析】
(1)根据题意和表格可以得到他批发600千克猕猴桃时,在A、B两家批发各需要花费多少钱,从而本题得以解决;
(2)根据题意和表格可以得到他批发x千克猕猴桃时(1500<x<2000),在A、B两家批发个需要花费多少钱,从而本题得以解决;
(3)将x=1800分别代入(2)求得的两个式子,计算出结果,然后进行比较,即可解答本题.
解:(1)由题意可得,
当批发600千克猕猴桃时,在A家批发需要:6×600×92%=3312(元),
当批发600千克猕猴桃时,在B家批发需要:6×500×95%+6×(600-500)×85%=2850+510=3360(元);
(2)由题意可得,
当他批发x千克猕猴桃(1500<x<2000),他在A家批发需要:6×x×90%=![]() (元),
(元),
当他批发x千克猕猴桃(1500<x<2000),他在B家批发需要:6×500×95%+6×(1500-500)×85%+6×(x-1500)×75%=2850+5100+4.5x-6750=![]() (元);
(元);
(3)现在他要批发1800千克猕猴桃,他选择在B家批发更优惠.
理由:当他要批发1800千克猕猴桃时,他在A家批发需要:5.4×1800=9720(元),
当他要批发1800千克猕猴桃时,他在B家批发需要:4.5×1800+1200=9300(元),
∵9720>9300,
∴现在他要批发1800千克猕猴桃,他选择在B家批发更优惠.


科目:初中数学 来源: 题型:
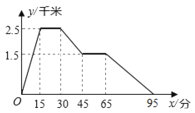
【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是:( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上,A、B两地相距300千米.甲乙两车分别从A、B两地同时出发,已知甲车速度为100千米/小时,乙车速度为60千米/小时.经过一段时间后,两车相距100千米,求两车的行驶时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a>![]() AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.

(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.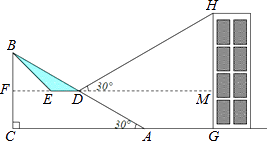
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com